Ламинарное и турбулентное течение

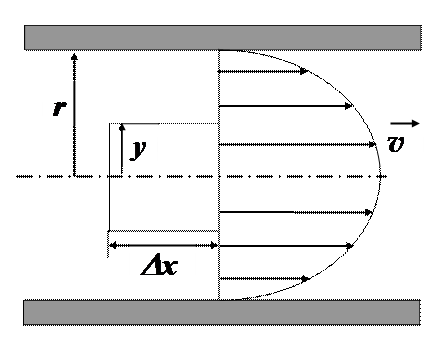
Рассмотрим течение смачиваемой жидкости по горизонтальной трубе круглого сечения радиусом r. Жидкость считаем несжимаемой и вязкой. Обозначим скорость течения в некоторой точке поперечного сечения трубы v, а расстояние этой точки от оси трубы обозначим y. Выделим внутри жидкости элементарный цилиндрический объём с осью, совпадающей с осью трубы, и боковой поверхностью, параллельной стенкам трубы и проходящей через точку с координатой y. Высоту цилиндра вдоль оси течения обозначим Dx. Так как движение стационарное и равномерное, то сила давления, действующая на основание цилиндрического объёма DP×py², и сила вязкости, действующая на боковую поверхность цилиндра

должны уравновешиваться.

 

 

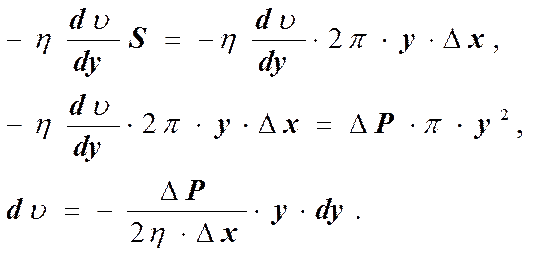(1)

После интегрирования, полагая, что у стенок имеет место прилипание жидкости, т.е. скорость на расстоянии равном r от оси скорость равна нулю (v_r = 0), и получим.

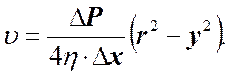(2)

Это соотношение устанавливает закон распределения скоростей течения в данном сечении трубы. Считая падение давления на единицу длины трубы постоянным (DP/Dx = const.) и объединяя постоянные получим выражение для скорости.

(3)

Т.е. скорость частиц жидкости распределяется в сечении трубы по параболическому закону. Вершина параболы лежит на оси трубы. Непосредственную опытную проверку этого закона провести сложно, так как любой измеритель скорости, помещённый в трубу, искажает распределение скоростей в месте измерения. Поэтому подсчитаем расход жидкости (количество жидкости, протекающей через сечение трубы за единицу времени) в предположении, что выражение (2) справедливо, а затем сравним его с фактически измеренным расходом. Так как скорость частиц жидкости зависит от их расстояния от стенок трубы, то мы подсчитаем элементарный расход жидкости через кольцевое сечение радиуса y и толщиной dy, в пределах которой скорость течения можно считать постоянной. За единицу времени через площадь кольцевого сечения вытекает объём жидкости.

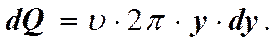(4)

Тогда с учётом (2) запишем.

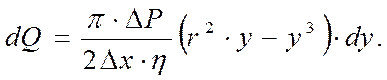(5)

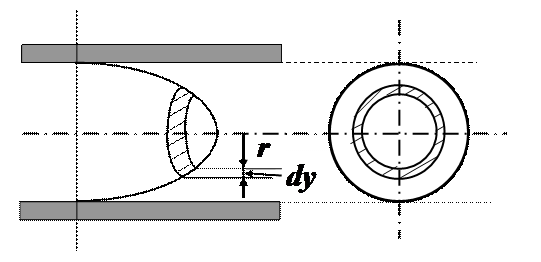
Интегрируя по всем кольцевым сечениям от 0 до r, получим расход жидкости в трубе.

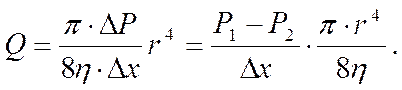(6)

Разделим расход жидкости на площадь сечения трубы S = p×r², получим среднюю скорость течения.

(7)

Эта зависимость называется законом Гагена-Пуазейля: средняя скорость параллельно струйного течения жидкости в трубе прямо пропорциональна падению напора на единицу длины трубы, квадрату радиуса трубы и обратно пропорционально коэффициенту вязкости жидкости.

Движение жидкости параллельными слоями называется ламинарным течением (от греческого "ламина" – слой).

Величина 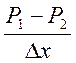– равна потере давления на единицу длины трубы.

Из (7) получим.

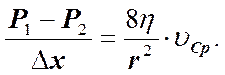
(8)

Т.е. сила сопротивления при ламинарном течении прямо пропорциональна первой степени скорости.

Проверка законом Гагена-Пуазейля осуществляется легко. При этом получается неожиданный результат. Уравнение (7) оказывается справедливым лишь при малых скоростях течения жидкости и малых размерах труб. Точнее говоря, при малых значениях некоторого безразмерного числа.

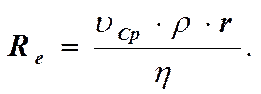(9)

В этом выражении: v_Ср – средняя скорость; r - плотность жидкости; h – коэффициент вязкости жидкости. Число R_e – носит название числа Рейнольдса.

При выводе закона Гагена-Пуазейля были использованы: второй закон Ньютона, применимость которого к движению жидкости не вызывает сомнения; закон Ньютона для вязкости, справедливость которого неоднократно проверялась. Следовательно, ошибочно какое-то предположение, которым пользовались. Осборн Рейнольдс (английский учёный) в 1883 г. впервые обнаружил, что условие параллельности скоростей жидкости выполняется при данных размерах трубы и для данной жидкости лишь до некоторого значения скорости (критическая скорость), выше которого течение теряет ламинарный характер.

Рейнольдс пускал в трубу с текущей жидкостью окрашенную струю. При достаточно малых значениях скорости течение было ламинарным, и краска двигалась резко очерченной струёй.

Но как только скорость течения жидкости достигала критического значения, струя краски быстро расходилась по всему сечению трубы виде вихревых образований – траектории частиц переставали быть параллельными и их скорости беспорядочно менялись как по величине, так и по направлению.

 

Представление (которое кажется самоочевидным) о том, что цилиндричность стенок трубы вынуждает все частицы жидкости двигаться параллельно им, в действительности, для скоростей, больших критических, не оправдывается.

 

При ламинарном течении: жидкость движется слоями, и скорости в каждом сечении параллельны друг другу; скорости частиц жидкости меняются от твёрдых границ внутрь потока по параболическому закону; сопротивление движению жидкости или твёрдого тела в ней прямо пропорциональна первой степени скорости, причём сопротивление обязано своим происхождением действию сил вязкости.

Если траектории частиц жидкости искривляются, то на них должна действовать некоторая сила, сообщающая им центростремительное ускорение. В потоке вязкой жидкости на каждую частицу действует сила давления F_P и сила вязкости F_В. Эти силы и обуславливают возникновение ускорения частиц. По второму закону Ньютона.

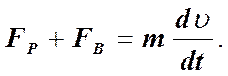(10)

Если система отсчёта связана с движущейся частицей, то в этой системе отсчёта на частицу будет действовать сила инерции, равная m×(dv/dt).

(Силы инерции мы рассмотрим позже).

Можно предположить, что степень устойчивости ламинарного течения характеризуется отношением сил инерции к силам вязкости, так как силы инерции, по-видимому, тем больше, чем больше отклонение траектории частиц в потоке от прямолинейного направления, а сила вязкости препятствует возникновению этих отклонений.

Силы инерции выражаются через произведение плотности жидкости на объём и на производную скорости по времени. Производную скорости по времени можно представить как величину, пропорциональную следующему отношению.

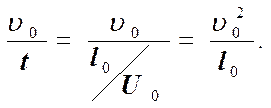(11)

v₀ – некоторая скорость, характерная для данной задачи. l₀ – некоторая характерная длина. Масса, т.е. произведение плотности на объём, пропорциональна r×l₀³. Тогда сила инерции будет равна.

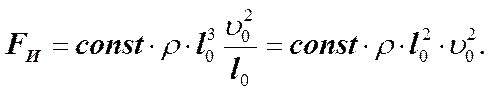(12)

Сила вязкости пропорциональна производной скорости по расстоянию – v₀/l₀, некоторой площади l₀² и коэффициенту вязкости h.

 

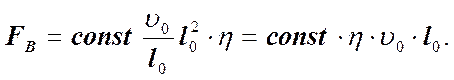(13)

Найдём отношение F_И к F _B. Легко видеть, что оно равно с точностью до постоянного множителя безразмерному числу, которое назвали числом Рейнольдса.

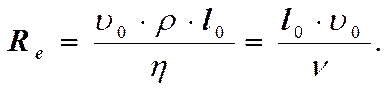(14)

v = h/r – коэффициент кинематической вязкости.

В число Рейнольдса (14) входит некоторая скорость v₀, размер l₀ и коэффициент кинематической вязкости. Коэффициент вязкости определён, если известна жидкость в потоке, для которого вычисляется значение R_e. Скорость v₀ есть скорость характерная для данного случая течения жидкости, например, для течения жидкости в длинной трубе – это средняя скорость в сечении трубы. Для случая обтекания жидкостью шарика – это скорость его движения относительно жидкости и т.д. Характерным размером в случае течения жидкости в трубе служит диаметр трубы. При обтекании малого по сравнению с размером потока шарика – это диаметр шарика и т.д.