Вязкость (внутреннее трение) мы рассмотрим позже.
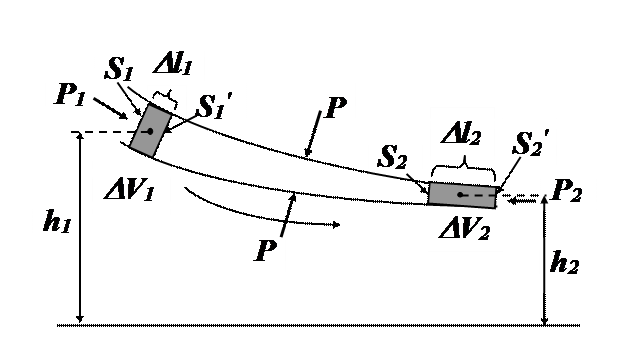
Выделим в стационарно текущей жидкости трубку тока малого сечения (см. рисунок). Рассмотрим объём жидкости, ограниченный стенками трубки тока и перпендикулярными к линиям тока сечениями S1 и S2. За время Dt этот объём переместится вдоль трубки, причём сечение S1 переместится в положение S1', пройдя путь Dl1, а сечение S2 переместится в положение S2', пройдя путь Dl2. В силу неразрывности струи, выделенные объёмы будут иметь одинаковую величину DV1 = DV2 = DV.
Энергия каждой частицы жидкости складывается из её кинетической энергии и потенциальной энергии в поле сил земного тяготения. Вследствие стационарности течения частица, находящаяся спустя время Dt в любой из точек выделенной части рассматриваемого объёма имеет ту же скорость (а, следовательно, и кинетическую энергию), какую имела бы частица, находящаяся в этой точке в начальный момент времени. Приращение энергии DЕ всего рассматриваемого объёма можно вычислить как разность энергий выделенных объёмов DV1 и DV2.
Возьмём трубку тока и отрезки Dl настолько малыми, чтобы всем точкам каждого выделенного объёма можно было приписать одно и тоже значение скорости v, давления Р и высоты h. Тогда приращение энергии запишется. (1)
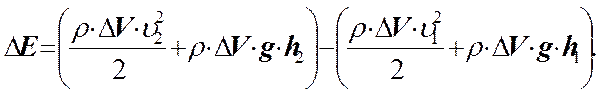
В этом выражении r – плотность жидкости.
В идеальной жидкости силы трения отсутствуют. Поэтому приращение энергии DЕ (из выражения 1) должно равняться работе, совершаемой над выделенным объёмом силами давления. Силы давления на боковую поверхность трубки тока перпендикулярны в каждой точке направлению перемещения частиц, к которым они приложены, и работы не совершают. Отлична от нуля лишь работа сил, приложенных к сечениям S1 и S2. Эта работа равна.
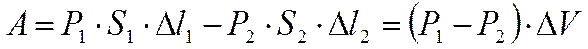(2)
Приравняем (1) и (2), сократим на DV и перепишем.
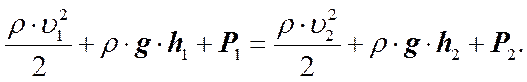(3)
Так как сечения S1 и S2 взяты произвольно, то можно утверждать, что в любом сечении трубки тока будет справедливо следующее выражение.
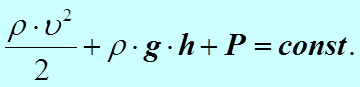(4)
Таким образом, в стационарно текущей жидкости вдоль любой линии тока выполняется условие (4), называемое уравнением Бернулли.
Это уравнение достаточно хорошо выполняется и для реальных жидкостей, вязкость которых не очень велика.
Рассмотрим некоторые следствия, вытекающие из уравнения Бернулли.
Если жидкость течёт так, что её скорость во всех точках одинакова, тогда из (3) получим.
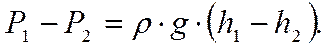
Т.е. распределение давления будет таким же, как в покоящейся жидкости.
Для горизонтальной линии тока (h1 = h2) уравнение (3) примет вид.
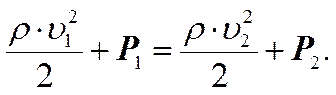
Т.е. давление оказывается меньше в тех точках текущей жидкости, где скорость больше.
Разберёмся с давлением.
Если поместить неподвижный манометр внутрь потока жидкости, то он будет также измерять давление в жидкости, но при этом характер потока, вследствие присутствия неподвижного манометра, изменяется.
В частности, если манометрическая трубка поставлена отверстием к потоку, то скорость жидкости перед отверстием равна нулю. Линии тока перед отверстием манометра расходятся, не попадая в область перед отверстием. Применим к этому случаю закон Бернулли, подставляя в (3) v2 = 0 и h1 = h2. В результате можно записать.
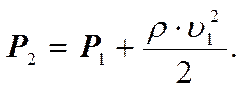
Т.е. неподвижный манометр, обращенный отверстием к потоку, измеряет давление большее, чем манометр, движущийся вместе с потоком. Избыток давления равен второму слагаемому в правой части последнего выражения. Происхождение этого избыточного давления совершенно очевидно. Частицы жидкости, останавливаясь перед манометром, сжимаются, и вследствие этого давление повышается. Создаётся "динамический напор".
Теперь мы можем дать себе отчёт о том, в каких случаях можно пренебрегать сжимаемостью газов. Наибольшее увеличение давления, которое может получиться при остановке потока, равно rv2/2, где v – максимальное значение скорости, встречающееся в потоке. Это избыточное давление обусловлено тем, что в местах остановки (или замедления) потока газ оказывается сжатым сильнее, чем в тех местах, где скорость потока наибольшая. Очевидно, что дополнительное сжатие газа будет тем менее заметно, чем меньше rv2/2 по сравнению с давлением Р в местах наибольшей скорости. Следовательно, дополнительное сжатие газа не играет существенной роли, пока rv2/2 << P, или до тех пор сжимаемостью газа можно пренебречь, пока наибольшие скорости в потоке малы по сравнению со скоростью звука в этом газе.
Применим уравнение Бернулли к случаю истечения жидкости из небольшого отверстия в широком открытом сосуде. Выделим в жидкости трубку тока, имеющую своим сечением с одной стороны открытую поверхность жидкости в сосуде, а с другой стороны – отверстие, через которое жидкость вытекает из сосуда. В каждом из этих сечений скорость и высоту над некоторым исходным уровнем можно считать одинаковыми, поэтому можно использовать уравнение (3).
Давление в обоих сечениях равно атмосферному давлению. Кроме того, скорость перемещения открытой поверхности в широком сосуде можно положить равной нулю. Тогда (3) можно переписать в следующем виде.
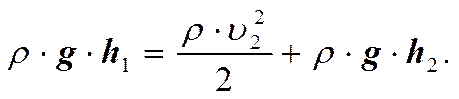
Сокращаем на плотность r и вводим v2 = v, учитываем, что h = h1 – h2 – высота открытой поверхности над отверстием. Получим.
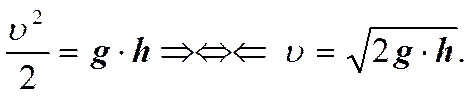(5)
Эта формула называется формулой Торричелли.
Итак, скорость истечения жидкости из отверстия, расположенного на глубине h под открытой поверхностью, совпадает со скоростью, которую приобретает тело, падая с высоты h. Это для идеальной жидкости. Для реальных жидкостей скорость истечения будет меньше, причём тем сильнее отличается от значения (5), чем больше вязкость жидкости.
Вязкость
При движении жидкостей и газов в них возникают силы внутреннего трения. Рассмотрим схему опыта. Возьмём две параллельно расположенные друг над другом горизонтальные стеклянные пластинки (обезжиренные и очищенные) со слоем воды или другой жидкости между ними. Верхнюю пластину приведём в движение. Слой жидкости, прилегающий непосредственно к верхней пластине, благодаря силам молекулярного сцепления прилипает к ней и движется вместе с пластинкой. Слой жидкости, прилипший к нижней пластинке, остаётся вместе с ней в покое. Промежуточные слои движутся так, что каждый верхний из них обладает скоростью большей, чем под ним лежащий.
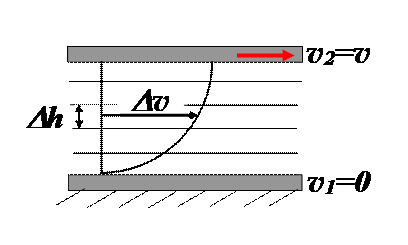Поэтому каждый верхний слой обладает относительно соседнего нижнего слоя скоростью, направленной в сторону движения пластинки. Нижний слой относительно верхнего движется со скоростью противоположного направления. Поэтому со стороны нижнего слоя на верхний действует сила трения, замедляющая движение второго из них, и обратно, со стороны верхнего на нижний – ускоряющая движение.
Силы, возникающие между слоями жидкости, испытывающими относительное перемещение, называют внутренним трением. Свойства жидкости, связанные с наличием сил внутреннего трения, называют вязкостью.
Если слои жидкости движутся с различными скоростями, то помимо того, что возникают силы взаимодействия между слоями молекул, смещающихся относительно друг друга, дополнительно возникает обмен импульсом между слоями в результате беспорядочного движения молекул. Молекулы, переходящие из слоя, обладающего большей скоростью, в слой, перемещающийся медленнее, увеличивают суммарный импульс во втором слое и, наоборот, молекулы переходящие из второго слоя в первый, уменьшают его суммарный импульс.
Взаимный обмен импульсом и взаимодействие молекул и создают внутреннее трение в жидкости. В газах внутреннее трение создаётся главным образом благодаря обмену импульсом.
Ньютон впервые предположил, что сила внутреннего трения между двумя слоями жидкости прямо пропорциональна разности скоростей Dv, площади их соприкосновения S и обратно пропорциональна расстоянию между слоями Dh.
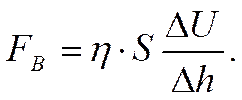(1)
h – коэффициент пропорциональности, называемый коэффициентом вязкости (динамическая вязкость). Величина обратная динамической вязкости называется текучестью. Существует также коэффициент кинематической вязкости v = h/r, где r – плотность жидкости.
В пределе для двух бесконечно близких слоёв.
градиент скорости (характеризует быстроту изменения скорости в направлении нормали к поверхности трущихся слоёв).
В СИ единица измерения коэффициента динамической вязкости (Н×с)/м2, или кг/(м×с), или Па×с.
Величина коэффициента вязкости меняется в зависимости от температуры. Вязкость газов с ростом температуры увеличивается, а жидкостей – уменьшается. Это и понятно, с ростом температуры увеличивается подвижность молекул и обмен импульсом между слоями газа. В жидкости этот обмен играет относительно меньшую роль, а межмолекулярное взаимодействие при повышении температуры и увеличении подвижности молекул ослабевает.
Вязкость в движении реальной жидкости сказывается двояко: во-первых, она создаёт передачу импульса от слоя к слою, благодаря чему скорости в потоке меняются от точки к точке непрерывно; во-вторых, переводит часть механической энергии потока в его внутреннюю энергию.
Для наглядности приведём таблицу коэффициента вязкости при атмосферном давлении от температуры для различных веществ.
| 0 оС | 18 оС | 99 оС | |
| Воздух | 1,72×10-5 | 1,83×10-5 | 2,17×10-5 |
| Спирт этиловый | 1,773×10-3 | 1,2×10-3 | _ |
| Глицерин | 12,1 | 1,48 | 0,013 |
