Элементы механики жидкости
Уравнение неразрывности струи
Чтобы описать движение жидкости или газа, можно задать траекторию и скорость как функцию от времени для каждой частицы жидкости (метод Лагранжа). Можно по-другому: следить не за частицами жидкости, а за отдельными точками пространства, фиксируя скорость, с которой жидкость или газ проходит через данную точку (метод Эйлера).
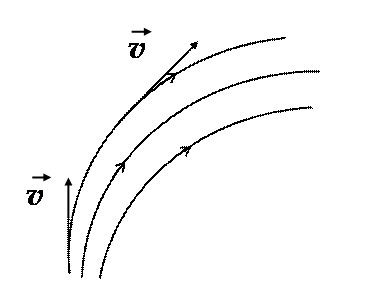Указав для каждой точки пространства вектор скорости, можно провести линию движения (траекторию частиц) жидкости или газа так, чтобы касательная к этой линии совпадала с направлением вектора скорости. Эти линии называются линиями тока.
Так как величина и направление вектора скорости могут меняться, то и картина линий тока может непрерывно меняться. Если вектор скорости в каждой точке пространства остаётся постоянным, то течение называется установившимся или стационарным. При этом любая частица жидкости проходит данную точку пространства с одним и тем же значением скорости.
Часть жидкости ограниченная линиями тока, называется трубкой тока. Частицы жидкости при своём движении не пересекают стенок тока.
Возьмём трубку тока настолько тонкую, что в каждом её сечении скорость можно считать постоянной. Предположим, что жидкость несжимаема, т.е. её плотность r всюду одинакова и не изменяется (не зависит от давления), то количество жидкости между сечениями S1 и S2 будет всегда неизменным.
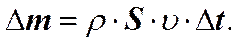
Тогда получим.
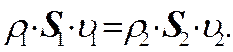
Отсюда следует, что объёмы жидкости (газа), протекающие за единицу времени через сечения S1 и S2, должны быть одинаковыми.
(1)
При стационарном течении не только жидкостей, но и даже газов изменениями плотности часто можно пренебречь и даже газы рассматривать как несжимаемые жидкости.
Для жидкости это верно в большинстве случаев. К течению газов это представление применимо пока скорости течения и искусственно создаваемые разности давлений невелики. Например, при течении газа под давлением, близким к атмосферному, и при скоростях порядка десятков метров в секунду, разность давлений в различных местах потока может изменяться только на сотые доли атмосферного давления. Эти разности давлений весьма существенны для всей картины в потоке, и ими нельзя пренебречь. Но относительно атмосферного давления, под которым находится газ, эти изменения давлений малы, и связанными с ними изменениями плотности газа вполне можно пренебречь. Поэтому во всех случаях, когда мы будем рассматривать стационарное течение жидкостей или газов, будем пренебрегать сжимаемостью не только жидкостей, но и газов. Для краткости мы дальше будем говорить о жидкостях, хотя все сказанное будет применимо к газам, пока можно пренебречь их сжимаемостью.
Результат, полученный в (1) применим к любой паре сечений. Следовательно, для несжимаемой жидкости в любом сечении одной и той же трубке тока всегда будет.
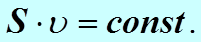
Это и есть уравнение или теорема о неразрывности струи.
Из последнего выражения следует, что там, где сечение трубки уменьшается, скорость потока возрастает. При переменном сечении трубки тока частицы несжимаемой жидкости движутся с ускорением.
Уравнение Бернулли
Данное уравнение получено известным швейцарским математиком и физиком, одним из представителей известной династии Бернулли, Даниилом Бернулли. Он в 1738 году опубликовал работу "Гидродинамика", где впервые привёл это уравнение. С 1725 года по 1733 год Даниил Бернулли работал в Петербургской Академии Наук.
Рассматривая движение жидкостей, во многих случаях можно считать, что перемешивание одних частей жидкости относительно других не связано с возникновением сил трения.
