Корреляция – это статистическая зависимость между случайными величинами, не имеющая строгого функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.
Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи).
Теснота связи количественно выражается величиной коэффициентов корреляции, которые, давая количественную характеристику тесноты связи между признаками, позволяют определять «полезность» факторных признаков при построении уравнения множественной регрессии.
Регрессия — статистическая зависимость среднего значения случайной величины от значений другой случайной величины или нескольких случайных величин.
Линейный коэффициент корреляции характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.
В теории разработаны и на практике применяются различные модификации формулы расчёта данного коэффициента:
.
Между линейным коэффициентом корреляции и коэффициентом регрессии существует определённая зависимость, выражаемая формулой
,
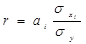где аi – коэффициент регрессии в уравнении связи;
хi – среднеквадратическое отклонение соответствующего, статистически существенного, факторного признака.
Линейный коэффициент корреляции изменяется в пределах от –1 до 1: -1 r 1. Знаки коэффициентов регрессии и корреляции совпадают.
Оценка линейного коэффициента корреляции
| Значение линейного коэффициента связи | Характер связи | Интерпретация связи |
| r = 0 | отсутствует | |
| 0 < r < 1 | прямая | с увеличением х увеличивается у |
| -1 < r < 0 | обратная | с увеличением х уменьшается уи наоборот |
| r = 1 | функциональная | каждому значению факторного признака строго соответствует одно значение результативного признака |
В случае наличия линейной и нелинейной зависимости между двумя признаками для измерения тесноты связи применяют так называемое корреляционное отношение. Различают эмпирическое и теоретическое корреляционное отношение.
Эмпирическое корреляционное отношение рассчитывается по данным группировки, когда 2 характеризует отклонения групповых средних результативного показателя от общей средней:
,
где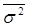 
– средняя из частных (групповых) дисперсий;
- корреляционное отношение;
2 – общая дисперсия;
2 – межгрупповая дисперсия (дисперсия групповых средних).
Все эти дисперсии есть дисперсии результативного признака.
Теоретическое корреляционное отношение определяется 
,
где 2 – дисперсия выравненных значений результативного признака, то есть рассчитанных по уравнению регрессии;
2 – дисперсия эмпирических (фактических) значений результативного признака.
Корреляционное отношение изменяется в пределах от 0 до 1 (0 1), и анализ степени тесноты связи полностью соответствует линейному коэффициенту корреляции.
Множественный коэффициент корреляции вычисляется при наличии линейной связи между результативным и несколькими факторными признаками, а также между каждой парой факторных признаков.
Множественный коэффициент корреляции для двух факторных признаков вычисляется по формуле
,
где r ух 
- парные коэффициенты корреляции между признаками.
Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен: 0 R 1.
Приближение R к единице свидетельствует о сильной зависимости между признаками.
Частные коэффициенты корреляции характеризуют степень тесноты связи между двумя признаками х1 и х2 при фиксированном значении других (k - 2) факторных признаков, то есть когда влияние х3 исключается, то есть оценивается связь между х1 и х2 в «чистом виде».
В случае зависимости у от двух факторных признаков х1 и х2 коэффициенты частной корреляции имеют вид
,
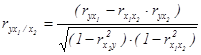где r – парные коэффициенты корреляции между указанными в индексе переменными. В первом случае исключено влияние факторного признака х2, во втором – х1.
