Ряды динамики - это значения статистических показателей, которые представлены в определенной хронологической последовательности.
Каждый динамический ряд содержит две составляющие:
1) показатели периодов времени (годы, кварталы, месяцы, дни или даты);
2) показатели, характеризующие исследуемый объект за временные периоды или на соответствующие даты, которые называют уровнями ряда.
Корректное применение в оценочной деятельности статистических методов выравнивания в конечном итоге приводит к более доказательным результата.
Метод простой скользящей средней - Заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем — средний уровень из такого же числа уровней, начиная со второго, далее — начиная с третьего, и т.д. Таким образом, при расчетах среднего уровня как бы скользят по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий. Отсюда название — скользящая средняя.

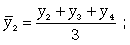
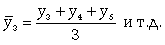
При изучении общей тенденции методом аналитического выравнивания исходят из того, что изменения уровней ряда динамики могут быть с той или иной степенью точности приближения выражены определенными математическими функциями. Задачей аналитического выравнивания является определение не только общей тенденции развития явления, но и некоторых недостающих значений как внутри периода, так и за его пределами. Способ определения неизвестных значений внутри динамического ряда называют интерполяцией. Эти неизвестные значения можно определить:
1)используя полусумму уровней, расположенных рядом с интерполируемыми;
2) по среднему абсолютному приросту;
3) по темпу роста.
Целью аналитического выравнивания является - определение аналитической или графической зависимости. На практике, по имеющемуся временному ряду, задают вид и находят параметры функции, а затем анализируют поведение отклонений от тенденции. Не следует смешивать выравнивание статистических рядов динамики со сглаживанием статистических рядов.
При использовании этого метода укрупнения интервалов ряд динамики, состоящий из мелких интервалов, заменяется рядом, состоящим из более крупных интервалов (например, преобразование месячных периодов в квартальные, квартальных в годовые и т.д.). Или уровни исходного динамического ряда объединяются по более крупным периодам. Так как на каждый уровень исходного ряда влияют факторы, вызывающие их разнонаправленное изменение, то это мешает видеть основную тенденцию. При укрупнении интервалов влияние факторов нивелируется, и основная тенденция проявляется более отчетливо. Расчет среднего значения уровня по укрупненному интервалу осуществляется по формуле простой средней арифметической. Недостаток этого способа заключается в том, что сокращается число уровней ряда, а это не позволяет учитывать изменения внутри укрупненного интервала. Но преимущество в том, что сохраняется природа явления.
По интервальным рядам итоги исчисляются путем простого суммирования уровней первоначальных рядов. Для других случаев рассчитывают средние величины укрупненных рядов (переменная средняя). Переменная средняя рассчитывается по формулам простой средней арифметической.






