В статистике индексами называются относительные показатели, выражающие изменения сложных экономических явлений, состоящих из непосредственно несуммируемых элементов.
Основным вопросом построения индексов является вопрос о сопоставимости сравниваемых явлений. Сопоставимость достигается различными способами. Наиболее простой из них – разложение сложных явлений на простые, однородные, а затем соизмерение этих простых явлений с помощью индивидуальных индексов (i).
Общий вид индивидуального индекса
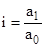, где 
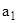- индексируемая величина, обычно отчетный уровень; 
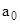- базисная величина.
Значительно сложнее, если необходимо соизмерить не отдельный элемент (цену, объем выпущенных одноименных и т.п.), а всю совокупность в целом. В этом случае необходимо использовать общие индексы (I), которые могут быть агрегатными или средними. В агрегатных индексах для разнородной совокупности находится такой общий показатель (агрегат), в котором можно объединить все ее элементы.
Агрегатный показатель представляет собой произведение качественного показателя (показывает экономическую сущность явления) и количественного (представляет объем изучаемой совокупности).
При построении агрегатных индексов существует правило: если индексируется (соизмеряется) качественный показатель, то весами к нему берется количественный в неизменном отчетном уровне; если индексируется количественный показатель, то весами берется качественный показатель в неизменном базисном уровне.
Согласно этому правилу агрегатный индекс цен (Ip) будет определяться по формуле
,
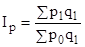где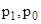 
- соответственно отчетный и базисный уровень цены; 
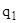- отчетный уровень количества продукции.
Агрегатный индекс объема продукции (индекс физического объема)
.
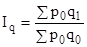Агрегатный индекс товарооборота (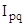
) можно определить двумя способами:
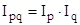или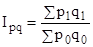 
.
Любой агрегатный индекс может быть преобразован в средний путем замены индексируемой величины индивидуальными индексами.
Например: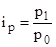 
, тогда 
; 
.
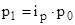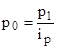Представив эти выражения в агрегатный индекс цен, можно получить:
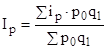- средний арифметический индекс цен;
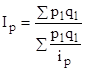- средний гармонический индекс цен.
Аналогично, меняя значения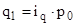 
и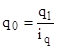 
, полученных из индивидуальных индексов объема, определяется:
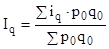- средний арифметический индекс физического объема;
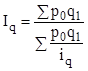- средний гармонический индекс физического объема.
Динамика общественных явлений может быть выявлена и охарактеризована при помощи сопоставления средних уровней. На величину показателей динамики среднего уровня оказывают влияние как изменение отдельных значений усредняемого признака, так и изменения их удельных весов.
Общая динамика среднего уровня называется индексом переменного состава (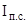
)
.
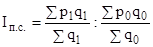Если значения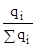 
заменить на показатель структуры 
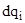, то индекс переменного состава примет вид
.
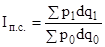Индексы среднего уровня, рассчитанные исходя из постоянной структуры, называются индексами фиксированного состава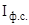 
, которые показывают изменение среднего уровня под влиянием изменений индивидуальных значений признака.
.
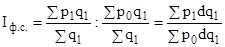Влияние структурных сдвигов на динамику среднего уровня определяется индексом структурных сдвигов (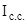
)
.
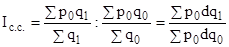Рассчитанные индексы находятся во взаимосвязи
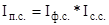
25. Понятие выборочного наблюдения.
Под выборочным наблюдением (сокращенно выборка) понимается не сплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергается не всё, а отдельные единицы, отобранные с соблюдением определенных условий.
