Выборочное статистическое наблюдение является наиболее широко применяемым видом не сплошного наблюдения. При выборочном методе обследованию подвергается сравнительно набольшая часть всей изучаемой совокупности (обычно до 5-10 %, реже до 15-20 %). При этом подлежащая изучению статистическая совокупность, из которой производится отбор части единиц, называется генеральной совокупностью. Отобранная из генеральной совокупности некоторая часть единиц, подвергающаяся обследованию, называется выборочной совокупностью или выборкой. Значение выборочного метода состоит в том, что при минимальной численности обследуемых единиц проведение исследования осуществляется в более короткие сроки и с минимальными затратами труда и средств. Это повышает оперативность статистической информации, уменьшает ошибки регистрации.
Под выборочным понимается метод статистического исследования, при котором обобщающие показатели изучаемой совокупности устанавливаются по некоторой ее части, организованной по принципу случайного отбора.
При случайном отборе каждой единице изучаемого объекта (массового явления, генеральной совокупности) обеспечивается определенная (обычно равная) вероятность попасть в количество обследуемых единиц (в выборку) и тем самым исключается субъективность, тенденциозность и односторонность в подборе этих единиц.
При строгом соблюдении принятых правил отбора выборочное наблюдение репрезентативно в широком смысле слова: при нем обеспечивается близкое соответствие состава охваченной наблюдением выборки и состава генеральной совокупности. Благодаря этому по данных выборочного наблюдения можно определить с желательной степенью приближения интересующие исследователей характеристики изучаемого явления.
Выборочный метод при проведении ряда исследований является единственно возможным, например, при контроле качества продукции (товара).
Выборочный метод иногда применяется для проверки данных даже сплошного учета. Минимальная численность обследуемых единиц позволяет провести исследование более тщательно и квалифицированно. Так, при переписи населения практикуются выборочные контрольные обходы для проверки правильности записей сплошного наблюдения.
Большую актуальность приобретает выборочный метод в условиях перехода к рыночной экономике. Развитие различных форм собственности, изменения в характере экономических отношений, как указывалось в предыдущих лекциях, обусловливают изменения функций учета и статистики, сокращение и упрощение статистической отчетности.
По сравнению с другими методами, применяющими не сплошное наблюдение, выборочный метод имеет существенное преимущество. При соблюдении правил научной организации выборочного наблюдения появляется возможность количественной оценки ошибки репрезентативности (представительности).
Более того, способы определения ошибок выборки при различных приемах формирования выборочной совокупности и распространение характеристик выборки на генеральную совокупность составляют основное содержание статистической методологии выборочного метода.
Проведение выборочного наблюдения складывается из ряда последовательных этапов:
1) обоснование целесообразности проведения выборочного метода в соответствии с задачами исследования;
2) составление программы проведения статистического исследования выборочным методом;
3) решение организационных вопросов сбора исходной информации;
4) установление доли выборки, т.е. части подлежащих обследованию единиц генеральной совокупности;
5) обоснование способов формирования выборочной совокупности;
6) осуществление отбора единиц из генеральной совокупности для их обследования;
7) фиксация в отобранных единицах выборки значений изучаемых признаков;
8) статистическая обработка полученной в выборке информации с определением обобщающих характеристик изучаемых признаков;
9) определение количественной оценки ошибки выборки;
10) распространение обобщающих выборочных характеристик на генеральную совокупность.
11) в зависимости от способа организации выборочного наблюдения и применяемых способов отбора различают также виды выборочного наблюдения:
1) простая случайная выборка (собственно-случайная);
2) механическая случайная выборка;
3) типическая случайная выборка;
4) серийная (гнездовая) выборка;
5) многоступенчатая (многостепенная или комбинационная) выборка.
Выборку можно производить из конечной (ограниченной) и неограниченной генеральной совокупности. Поэтому целесообразно различать выборочный метод и по этому признаку. Иногда различают также большие, охватывающие значительное число обследуемых единиц, выборки и малые выборки.
Каждый из указанных основных способов отбора может реализоваться по схеме повторного (когда зафиксированная в выборке единица возвращается в генеральную совокупность) или бесповоротного отбора (когда зафиксированная единица исключается из дальнейшего просмотра и может попасть в выборку только один раз). Целесообразно различать выборки и по этому признаку.
Ошибка выборки
Расхождения между характеристиками выборочной и генеральной совокупности принято называть ошибкой выборки.
В математической статистике доказывается, что значение усредненной ошибки выборки (
) определяется по формуле
,
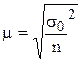где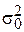 
- генеральная дисперсия;
- объем выборки.
В этой формуле, как видно из записи, предполагается, что генеральная дисперсия известна. Но в выборочном обследовании она неизвестна. Поэтому на практике вместо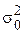 
используют дисперсию выборочной совокупности 
. Дело в том, что при соблюдении основных принципов организации и проведения выборочного наблюдения (случайного отбора, обоснования объема выборки) дисперсия достаточно большого объема выборки стремится отобразить дисперсию генеральной совокупности.
При этих условиях зависимости между дисперсиями в генеральной и выборочной совокупностях выражается так:
.
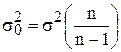Отсюда видно, что если n достаточно велико, то отношение
.
Например, при n = 100 оно равно 1,01 и при n = 500 уже имеем = 1,002 и т.д.
С учетом рассмотренного расчет средней ошибки выборки можно проводить по формуле
.
Для альтернативного признака дисперсия в выборочной совокупности определяется по формуле
.
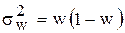Для количественного признака соответственно используется формула
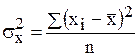или 
.
Строго говоря, указанные выводы верны только для так называемого повторного отбора (см. п. 12.4 данной темы), т.е. когда каждая попавшая в выборку единица совокупности после фиксации должна быть возвращена в генеральную совокупность и ей представляется равная возможность снова попасть в выборку. Однако на практике выборочное наблюдение проводится, как правило, по схеме бесповторного отбора.
Поскольку при бесповторном отборе численность генеральной совокупности N в ходе выборки сокращается, то в формулу для расчета средней выборки включается дополнительный множитель
.
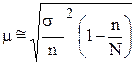С учетом полученной оценки средней ошибки выборки истинное значение характеристики генеральной совокупности определяется по формуле
.
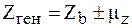В общем виде это записывается так:
.
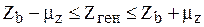Другими словами, полученные характеристики выборочной совокупности отличаются от характеристики генеральной совокупности на величину средней ошибки выборки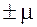 
.
Следует иметь в виду, что такое утверждение можно гарантировать лишь с определенной степенью вероятности, а не с абсолютной достоверностью.
В математической статистике доказывается, что эта вероятность равна 0,683. Это означает, что в 683 случаях на 1000 генеральной характеристики будут находиться в указанных выше пределах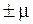 
. В остальных же 317 случаях они могут выйти за эти пределы.
Вероятность суждения можно повысить, если расширить пределы отклонения (если среднюю ошибку выборки увеличить в t раз).
Так, при t = 2 вероятность суждения надежности достигает 0,954. А при t=3 вероятность суждения повышается до 0,997.
Таким образом, показатели характеристики генеральной совокупности определяются по формуле
.
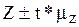В статистике множитель t называется коэффициентом доверия.
Русский математик А.М.Ляпунов (1857-1918) обосновал математическое выражение конкретных значений множителя t для различных степеней вероятности в виде функции:
.
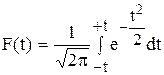На практике пользуются готовыми таблицами этой функции применительно к случаю нормального распределения.
Например.
| Кратность ошибки t | Вероятность F(t) | Кратность ошибки t | Вероятность F(t) |
| 0,0 0,1 0,5 1,0 1,5 | 0,000 0,0797 0,3829 0,6827 0,8664 | 2,0 2,5 2,6 3,0 4,0 | 0,9545 0,9876 0,9907 0,9973 0,999937 |
Выбор той или иной доверительной вероятности зависит от необходимой степени достоверности результатов выборочного наблюдения. В экономических исследованиях обычно ограничиваются значениями t, не превышающими 2-3 единиц.
Если примем t=2.6, то имеем в 99 случаях из 100 характеристика генеральной совокупности будет совпадать с соответствующей выборочной характеристикой, т.е. будет находиться в пределах
.
Гарантия результатов выборочных обследований в 99 случаях из 100 практически равнозначна достоверности.
Обобщим полученные выводы.
Итак, по своей природе характеристики выборочной совокупности являются случайными величинами.Они могут принимать различные значения в зависимости от конкретных единиц генеральной совокупности, попавших в выборку. Однако каждый из возможных результатов выборки имеет определённую вероятность; соответственно и каждая из возможных ошибок выборки. Поэтому средняя ошибка выборки есть средняя квадратическая величина, взвешенная из отдельных ошибок вероятности их возникновения.
Получили, что предельная ошибка выборки (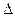
) связана со средней ошибкой выборки (
) отношением для повторной схемы отбора: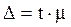 
.
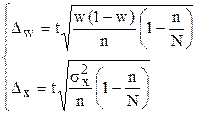