Способы отбора единиц из генеральной совокупности

 

В статистике для формирования выборочной совокупности с учетом задач исследования и специфики объекта изучения могут применяться различные способы.

Основным условием проведения выборочного обследования является предупреждение возникновения систематических (тенденциозных) ошибок. Для этого надо обеспечить реализацию принципа равных возможностей попадания в выборку каждой единицы генеральной совокупности.

Практика применения выборочного метода в экономико-статистических исследованиях различает следующие основные способы отбора единиц из генеральной совокупности:

1. Индивидуальный отбор – в выборку отбираются отдельные единицы генеральной совокупности;

2. Групповой отбор – в выборку попадают качественно однородные группы или серии изучаемых единиц

3. Комбинированный – как комбинация индивидуального и группового отбора.

Как указывалось выше, способы отбора определяются правилами формирования выборочной совокупности. Здесь в связи с этим уместно вспомнить основные виды выборок:

· Собственно-случайная;

· Механическая случайная;

· Типическая;

· Серийная;

· Многоступенчатая.

Собственно-случайная выборка образуется в результате случайного (непреднамеренного) отбора единиц из генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц обычно определяют исходя из принятой доли (процента) выборки.

Доля выборки есть отношение числа единиц выборочной совокупности n к числу единиц в генеральной совокупности N

 

.

 

Так, при 5%-ной выборке из партии в 2000 ед. численность выборки составляет n=100 ед. , а при 20%-ной выборке n=400 ед. .

Одним из примеров использования собственно-случайной выборки является проведение выигрышной денежно-вещевой лотереи, при которой обеспечивается равная возможность попадания в тираж любого номера лотерейного билета.

Формирования собственно-случайной выборки может осуществляется с помощью специальных фишек (с номерами единиц генеральной совокупности) одинаковой формы или таблицы случайных чисел.

Собственно-случайная выборка может быть осуществлена по схемам повторного и бесповторного отбора.

При повторном отборе каждая единица, попавшая в выборку после её фиксации (включенная в выборку), должна обратно возвратиться в генеральной совокупность.

Например, при изучении покупательского спроса населения не исключена повторная регистрация спроса одного и того же лица в нескольких магазинах города. Однако при тестировании качества электролампы одна и та же лампа не может быть подвержена повторной проверке на продолжительность горения. Возвращать в генеральную совокупность лампочки с перегоревшими нитями не имеет смысла. Поэтому на практике чаще применяются схемы бесповторного отбора.

При бесповторном отборе единица, попавшая в выборку, исключается из генеральной совокупности и дальнейший отбор осуществляется. из оставшихся единиц.

Механическая выборка состоит в том, что отбор единиц в выборку производится из генеральной совокупности, разбитой на равные группы (интервалы).

Размер интервала равен обратной величине доли выборки. Так, при 2%-ной выборке отбирается каждая 50-я единица (1:0,02) и т.д.

Таким образом, в соответствии с принятой долей отбора ген совокупность как бы механически разбивается на равновеликие группы и из каждой группы в выборку отбирается лишь одна единица.

Возникает вопрос: как расположить единицы в генеральной совокупности? Ведь от этого будет зависеть репрезентативность выборки. Как показывает практика, по отношению к изучаемому показателю единицы генеральной совокупности могут быть упорядочены по существенному, второстепенному или нейтральному признаку.

При упорядочении по существенному признаку (который всецело определяет поведение изучаемого показателя), в выборочную совокупность должна отбираться та единица, которая находится в середине каждой группы.

При упорядочении по нейтральному признаку (не оказывает влияние на поведение изучаемого признака) в выборку может быть взята любая единица из каждой группы. Для соблюдения принципа случайного отбора во всех группах механической выборки берут те номера единиц, которые отобраны в первой группе.

При упорядочении единиц генеральной по совокупности второстепенным признакам (лишь частично могут оказать влияние на изучаемый признак) целесообразно для исключения систематической ошибки выборки также отбирать единицы, находящиеся в середине группы.

Важной особенностью механической выборки является то, что формирование выборочной совокупности можно осуществит, не прибегая к составлению списков. Например, используем порядок фактического размещения единиц генеральной совокупности (последовательность выход готовых изделий с конвертера, порядок размещения партии товаров при хранении и т.д.).

Величина средней ошибки механической выборки теоретически должна определяться с учетом показателя внутригрупповых дисперсий. Однако из практики доказано, что механическая выборка по точности результата очень близко подходит к собственно случайному способу отбора. Поэтому для определения средней ошибки механической выборки обычно используются формулы собственно случайной бесповторной выборки.

При типической выборке генеральная совокупность вначале расчленяется на однородные типические группы. Затем из каждой типической группы собственно случайным или механическим способом производится индивидуальный отбор единиц в выборочную совокупность.

Типическая выборка обычно применяется для изучения сложных совокупностей. Например, при изучении производительности труда работника с учетом их уровня квалификации или профессии.

Как показывает практика, типическая выборка дает более точные результаты по сравнению с другими способами отбора единиц.

Группировку можно производить по результатам исследований из сущности изучаемого явления или использовать уже имеющиеся классификации и группировки. Ведь ясно, что чем однороднее состав образованных типических групп, тем лучше типическая выборка будет воспроизводить характеристику изучаемого признака в генеральной совокупности.

При определении ошибки типической выборки в качестве показателя вариации выступает средняя из внутригрупповых дисперсий.

Для доли альтернативного признака она вычисляется по формуле

 

;

 

и для средней величины количественного признака применяется формула

 

.

 

На практике типическая выборка формируется пропорционально численности единиц, составляющих типические группы. Поэтому для определения средней ошибки типической выборки используют формулы

а) для доли альтернативного признака

повторный отбор ;

бесповторный отбор ;

б) для средней величины количественного признака

повторный отбор ;

бесповторный отбор .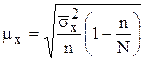

(**)Довольно широкое применение находит так называемая серийная или гнездовая выборка. При этом способе генеральная совокупность разбивается на серии и в случайном порядке отбираются целые гнезда, в которых производится сплошное обследование.

Например, при контроле качества товара рациональнее проверить несколько отдельных упаковок, чем из всех упаковок отбирать необходимое количество единиц товара.

Отбор отдельных серий осуществляется или посредством собственно случайной выборки или механическим отбором. Обычно серийная выборка производится по схеме бесповторного отбора.

Для определения средней ошибки серийной выборки применяются следующие формулы

а) для количественного признака ,

где межсерийная дисперсия выборки ; R и r – число серий в выборке и генеральной совокупности;

б) для альтернативного признака ,

где - межсерийная дисперсия выборочной доли.

(***)По сравнению с типической выборкой серийная выборка дает более высокую ошибки репрезентативности, т.к. обследуется сравнительно небольшое число серий.

Как видели в рассмотренных способах выборки осуществляется:

1. Индивидуальный отбор – в выборку отбираются отдельные единицы генеральной совокупности (при собственно-случайном и механическом)

2. Групповой отбор – в выборку попадают качественно однородные группы как серии изучаемых единиц (0 в серийном отборе

3. Однако на практике эти способы применяются комбинированно в различных сочетаниях и с различной последовательностью. Так, например, в серийной выборке:

· Случайным или механическим способом отбираются отдельные серии;

· В выборку включаются все единицы отобранных серий или одинаковые доли единиц из каждой серии.

Средняя ошибка комбинированной выборки складывается из соответствующих средних ошибок применяемых способов.

Например, разбиваем всю совокупность на группы и затем осуществляем гнездовой отбор.

Средняя ошибка для такой комбинированной выборки определяется по формулам:

а) при повторном отборе ;

б) при бесповторном отборе .

В статистике различают также одно- и многоступенчатые способы отбора единиц в выборочную совокупность.

При одноступенчатой выборке каждая отобранная единица сразу же подвергается изучению по заданному признаку.

При многоступенчатой выборке производится отбор из генеральной совокупности отдельных групп, а из групп выбираются отдельные единицы. Например, типическая выборка с механическим способом отбора единиц в выборочную совокупность.

Комбинированная выборка может быть двухступенчатой (разбиение на группы, отбор групп и внутри последних отбор отдельных единиц) и многоступенчатой (отбор групп, затем из них отбор средних, мелких и в внутри последних отбор отдельных единиц). Например, при бюджетных обследованиях семей используется трехступенчатый отбор (отбор районов, отбор населенных пунктов, отбор семей). При этом на отдельных ступенях могут изменяться и виды выборки. Следует иметь в виду, что при многоступенчатой выборке производится отбор самих групп, поэтому не все они попадают в выборку.

Средняя ошибка выборки при многоступенчатом отборе определяется по формуле

 

,

 

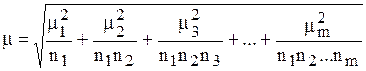где ошибка выборки на смещениях - численность выборки по ступени отбора

 

Малая выборка

 

Как видели из предыдущих параграфов, в зависимости от задач исследования в выборках может быть включено различное количество единиц изучаемой совокупности. Если n>100, то выборочное наблюдение считается со сравнительной большим объёмом выборки. А если n<100, то стат. Обследование принято называть малой выборкой.

Под малой выборкой понимается стат. обследование, при котором выборочная совокупность образуется из сравнительно небольшого числа единиц генеральной совокупности.

Объём малой выборки обычно не превышает 30 единиц и может доходить до 4-5 единиц

На практике к малой выборке прибегают, когда бывшая выборка нецелесообразна (например, если проведение исследования связано с уничтожением или порчей обследуемых образцов) или невозможна (при экспресс-обследование)

Из-за небольшого объема выборки величина ошибки малой выборки определяется по спец. Формуле

 

,

 

где дисперсия малой выборки.

Вспомним соотношение между дисперсиями в ген. совокупности () и выборочной совокупности ():

 

.

В малой выборке имеет существенное значение, то вычисление дисперсии малой выборки производится с учётом так называемого числа степеней свободы. Под числом степеней свободы понимается количество вариантов, которые могут принимать произвольные значения, не меняя величины средней.

При определении дисперсии числа степеней свободы равно (n-1)

 

.

 

Предельная ошибка малой выборки (ЦЦЦ) определяется по формуле

 

.

 

При этом значение коэффициента доверия (t) зависит не только от заданной доверительной вероятности, но и от численности малой выборки (n). Для этих целей исп. специальная таблица (таблицы Стьюдента). В этих таблицах даны распределения стандартизованных отклонений

 

.

 

Таблица Стьюдента приводится в учебниках по математической статистике или сборниках специальных математических таблиц.

Приведём фрагмент этой таблицы

 

k=n-1	t
0,5	1,0	1,5	2,0	3,0
	0,347 0,362 0,368 0,371 0,376 0,377	0,609 0,637 0,649 0,657 0,667 0,670	0,769 0,806 0,823 0,832 0,846 0,850	0,861 0,898 0,914 0,923 0,936 0,940	0,942 0,970 0,980 0,983 0,991 0,993

Как видно из этих таблиц, что при увеличении объёма выборки распределение Стьюдента приближается к нормальному и уже при n=20 оно мало отличается от нормально распределения. Отсюда же видно, что чем меньше объём выборки, тем больше это различие и например, при n=4 это различие весьма существенно. Следовательно уменьшается точность результатов малой выборки.

Пример. Допустим отобрано 10 рабочих для определения времени выполнения ими определённой операции. Среднее время у них оказалось равным 10,4 мин и дисперсия выборки 4. Примем доверительную вероятность р= 0,984.

 

Решение.

По таблице распределения Стьюдента t=3 определим отсюда . Доверительный интервал 6,4<x<12.4.

 

Малая выборка

Оздоровительный центр рекламируя свои услуги, предлагает за короткий срок снижение веса. По результатам выборочного обследования 15 женщин, воспользовавшихся услугами центра, были получены следующие данные о снижении их веса.

 

№ n/n
снижение веса, кг	10,2	7,6	8,4	6,0	5,7	13,7	6,9	5,2	6,1	5,0	3,7	4,7	3,6	6,1	3,2

 

Необходимо проверить обоснованность таких реклам с вероятностью 0,99 (t=2.977).

Решение:

1) находим выборочное среднее

2) выборочная дисперсия составляет

3) средняя квадратическая ошибка выборки равна

4) находим предельную ошибку

Отсюда снижение веса пациентов оздоровительного центра будет находиться в пределах .

Или от 4,23 до 8,59 кг.

Следовательно, указанное в рекламе снижение веса на 10 кг имеет весьма малую вероятность и даже событие практически не возможное.

 

Вывод формулы разложения общего прироста выпуска продукции по трудовым факторам.

Из зависимости показателей .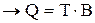

 

 

порядок подставок:

а) изменение работников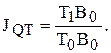

 

 

б) изменение Пт

 

 

преобразуем эту запись б

 

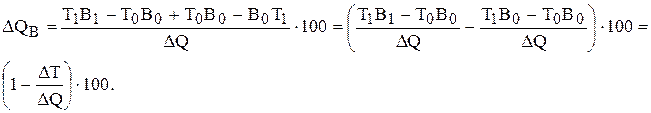
расчёт в %

год

5 лет .

 

Ежегодно: за пять лет .

 

Годы
	1,00	1,10	1,21	1,33	1,46	1,60
	1,00	1,10	1,21	1,33	1,46	1,60
	1,00	1,21	1,46	1,77	2,13	2,56

 

Задача № 23 + пример.

Задача 20. (B и t).

Задача 24, Территориальный индекс а изменение валового стада в районе А по сравнению с районом Б

Проверим правильность выводов путём замены .

 

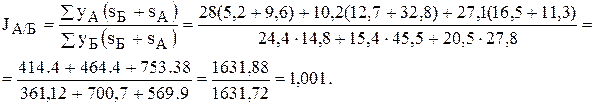
Контрольные вопросы по теме 12

 

1. В чем преимущества выборочного метода в сравнении с другими видами несплошного наблюдения?

2. Какие преимущества и недостатки имеет метод выборочного наблюдения по сравнению с сплошным статистическим наблюдением?

3. Какие способы формирования выборочной совокупности Вы знаете Дайте краткую характеристику им.

4. Что означает ошибка репрезентативности и какие факторы определяют ее величину?

5. От чего зависит точность оценки параметров генеральной совокупности (генеральной средней и генеральной доли)?

6. Чем отличается величина усредненной ошибки простой случайной выборки при повторном и бесповторном отборе? Какая из этих ошибок больше?

7. Чем отличается ошибка простой случайной выборки при проведении больших и малых выборок?

8. Как определяется предельная ошибка при проведении большой и малой выборки?

9. В чем различие механического способа отбора по сравнению с простым случайным (собственно-случайным отбором? Как определяется величина стандартной (средней) ошибки механической выборки?

10. В чем специфика организации механического отбора при систематизации единиц генеральной совокупности по существенному, второстепенному и нейтральному признакам?

11. Какой вид выборочного наблюдения следует использовать, если генеральная совокупность не является однородной?

12. В чем состоят преимущества серийной выборки перед простой случайной выборкой?

13. Как должна формироваться выборочная совокупность при проведении типической выборки?

14. Как определяется усредненная ошибка типической и серийной выборок?

15. Какие способы распределения выборочных характеристик Вам известны? Дайте краткую характеристику и назовите наиболее целесообразные области их применения.

16. Запишите доверительные интервалы генеральной средней с вероятностью 0,95 и 0,99.

17. В чем состоит проблема определения оптимальной численности выборки?

18. Для решения каких вопросов организации выборочного наблюдения и оценки его результатов может использоваться формула средней ошибки выборки?

19. Чем отличается величина относительной численности выборки простой случайной выборки при повторном и бесповоротном отборе? Какая из этих величин больше?

20. Назовите важнейшие области применения выборного метода в практике государственной статистики.

 

ТЕМА 13. КОРРЕЛЯЦИОННАЯ СВЯЗЬ И
ЕЕ СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ

 

13.1. Предпосылки изучения корреляционной связи.

13.2. Статистические методы выявления корреляционной связи.

13.3. Статистическое измерение тесноты корреляционной связи. Показатели меры тесноты корреляционной связи.

13.4. Корреляция рангов.

13.5 Множественная и частная корреляция.

13.6. Статистические исследования формы корреляционной связи. Линия регрессии и уравнение регрессии.

13.7. Статистическое исследование зависимости между качественными признаками.

13.8. Изучение корреляционной зависимости между рядами динамики.

Контрольные вопросы по теме 13.