XIV. Движение границы раздела двух

ЖИДКОСТЕЙ С УЧЕТОМ НЕПОЛНОТЫ ВЫТЕСНЕНИЯ.

ТЕОРИЯ БАКЛЕЯ - ЛЕВЕРЕТТА

 

При проектировании разработки и эксплуатации нефтяных и газовых месторождений большое внимание уделяется задачам движения границы раздела двух жидкостей в пористой среде. Например, в нефтяных пластах, разрабатываемых при водона­порном режиме, вода обычно не заполняет полностью область, первоначально занятую нефтью. В этой области происходит одновременное движение вторгшейся воды и оставшейся, постепенно вымываемой нефти.

Решение такого важного вопроса, как повышение коэффи­циента нефтеотдачи нефтяных месторождений, разрабатывае­мых при поддержании пластового давления закачкой в пласт воды или другого вытесняющего нефть агента, связано с зада­чами фильтрации многокомпонентных жидкостей.

При фильтрации двухфазной жидкости для каждой фазы в •отдельности справедлив закон Дарси. В общем случае при нали­чии массовых сил фильтрация двухфазной несжимаемой смеси описывается (по числу неизвестных )следующей замкнутой системой уравнений:

(XIV.1)

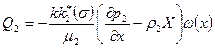(XIV.2)

(XIV.3)

(XIV.4)

(XIV.5)

где σ — насыщенность порового пространства первой (вытесняю­щей) фазой; р₁ и р₂ — соответственно давления каждой фазы, которые, вообще говоря, не равны друг другу из-за капилляр­ных эффектов; X — проекция массовых сил, отнесенная к еди­нице массы; р_к(σ) —капиллярное давление; R₁ и R₂ — в фор­муле Лапласа (XIV.3) — главные радиусы кривизны менисков контактной поверхности, зависящие, в основном, от насыщен­ности; а — поверхностное натяжение. Остальные обозначения прежниеНа практике капиллярное давление считается известной экс­периментальной функцией насыщенности и представляется в виде зависимости безразмерной функции Леверетта от насыщенности σ порового простран­ства вытесняющей жидкостью (рис. 89), θ — статический крае­вой угол между жидкостями и породой.

 

 

 

 

Оценки, сделанные М. Маскетом, показывают, что в пласте градиент капиллярного давления обычно мал по сравнению с градиентом гидродинамического давления всюду, кроме зоны фронта вытеснения, где насыщенность а резко изменяется, a поэтому имеют место большие значения градиента капиллярного давления (см. рис. 89), которые необходимо учитывать. Однако из-за исключительной сложности решения задач двухфазной фильтрации оба эти фактора не принимаются во внимание, а капиллярность косвенно учитывается самим видом экспери­ментальных кривых для несцементированных и слабо сцементированных песков (рис. 90); на графиках , .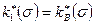

Наиболее разработанной теорией является теория одномер­ного движения двухфазной жидкости в пористой среде Баклея — Леверетта. Рассматривая двухфазную фильтрацию в трубке тока по­стоянного сечения при отсутствии капиллярного давления и без учета массовых сил и полагая, что суммарная скорость фильт­рации является постоянной величиной: , Баклей и Леверетт из системы уравнений (XIV.1)—(XIV.5) получили дифференциальное уравнение относительно σ

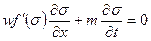(XIV.6)

где т — пористость пласта; — производная от функции Леверетта

, (XIV.7)

Уравнение (XIV.6) является квазилинейным дифференциаль­ным уравнением 1-го порядка в частных производных.

Решение уравнения (XIV.6) имеет вид:

(XIV.8)

где — координата точки с заданной насыщенностью σ в момент t = 0.

Уравнение (XIV.8) определяет перемещение точки с задан­ной насыщенностью с течением времени.

Скорость распространения заданной насыщенности σ полу­чим из уравнения (XIV.8), взяв производную dx/dt,

(XIV.9)

Функция Леверетта f(σ) и ее производная представ­лены на рис. 91. Как видно из графика, одному и тому же значению , определяющему скорость распространения на­сыщенности заданной величины, соответствуют два разных значения насыщенности σ.

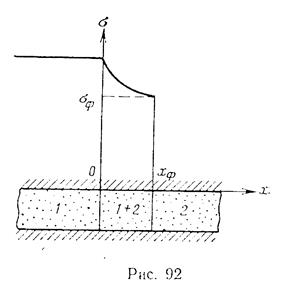
Это означает, что, начиная с некоторого момента, распреде­ление насыщенности становится многозначным, а это физически невозможно. Многозначность означает, что в зоне движения двухфазной жидкости имеет место скачок насыщенности (рис. 92).

Баклей и Леверетт из условия материального баланса полу­чили формулу для определения значения фронтовой насыщен­ности σ_ф (насыщенности на скачке)

(XIV.10)

Очевидно, что фронтовую насыщенность σ_ф можно легко определить графически. Проведя из начала координат каса­тельную к кривой f(σ) (рис. 93) и опустив перпендикуляр из точки касания на ось σ, получим значение фронтовой насыщен­ности.

Подставив σ_ф в (XIV.8), можем найти координату скачка насыщенности .

 

 

 

 

Чтобы найти среднее значение насыщенности в переходной зоне, разделим объем поступившей вытесняющей жидкости на объем порового пространства переходной зоны, определяемого координатой при площади поперечного сечения пласта, рав­ной единице,

(XIV.11)

Среднюю насыщенность σ_ср можно определить графически следующим образом. Если продлить касательную к кривой f(σ) до пересечения с прямой f(σ) =1, то значение σ в точке пере­сечения и есть средняя насыщенность σ_ср (см. рис. 93).

Как правило, среднее значение насыщенности порового про­странства водой σ_ср значительно меньше единицы. Поэтому, на­пример, в процессах вытеснения нефти водой для более полного извлечения нефти из пласта на объем добытой нефти нужно закачать несколько объемов воды.

 

Задача 122

 

Построить функцию Леверетта f(σ) в случае, если зависи­мости относительных фазовых проницаемостей нефти и воды от насыщенности водой порового пространства σ за­даются кривыми Леверетта (см. рис. 90), отношение .

Решение. Задаемся рядом значений σ, для каждого зна­чения σ по графику Леверетта (см. рис. 90) определяем соот­ветствующие и ; подставляя их в (XIV.7), подсчитываем f(σ) и строим график f(σ) (см. рис. 93). Результаты расчетов приведены ниже.

σ, %........0 10 20 30 40 50 60 70 80 90 100

..........- - 0,70 0,50 0,34 0,23 0,13 0,06 0,02 0 0

..........0 0 0 0,01 0,05 0,11 0,21 0,33 0,51 0,72 -

f(σ).......0 0 0 0,074 0,37 0,66 0,87 0,96 0,99 1 1

 

Задача 123

 

Используя полученный в задаче 122 график функции Леве­ретта (см. рис. 93), определить значение фронтовой насыщен­ности σ_ф и средней насыщенности σ_ср порового пространства водой в зоне вытеснения нефти водой.

Решение. Для определения фронтовой насыщенности σ_ф из начала координат проведем касательную к кривой, выражающей функцию Леверетта (см. рис. 93). Значение насыщенности в точке касания соответствует фронтовой насыщенности σ_ф = 59%.

Значение средней насыщенности найдем, продолжая каса­тельную к кривой f(σ) до пересечения ее с горизонтальной прямой f(σ) = 1. Значение насыщенности в точке пересечения касательной с прямой f(σ) =1определяет значение σ_ср = 69%.

 

Задача 124

 

В однородном по мощности, пористости и проницаемости пласте происходит прямолинейно-параллельное вытеснение нефти водой по закону Дарcи. Определить положение фронта вытеснения в различные моменты времени, если пористость пласта m = 20%, отношение , дебит галереи Q = 21,6·10³ м³/сут, ширина фильтрационного потока В = 500 м, мощность пласта h =10 м. Зависимости относительных прони­цаемостей нефти и воды от насыщенности порового простран­ства водой задаются графиками Эфроса, для которых графики функции Леверетта f(σ) и ее производной представлены: на рис. 94 и95.

Насыщенность пласта связанной водой составляет σ_св = 18%.

Решение. Определим значение σ_ф, для чего проведем из начала координат касательную к кривой f(σ) (см. рис. 94). Как видно из чертежа, σ_ф =0,84 и соответствующее значение производной =1,4 (см. рис. 95). Суммарная скорость фильт­рации

 

 

 

 

 

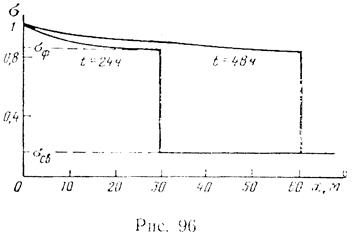
Задаваясь различными значениями t, подсчитаем no (XIV.8) координат фронта вытеснения , учитывая, что в начальный момент времени :

Результаты вычислений приведены ниже.

t, ч………1 12 24 48 240

, м…...1,16 15,1 30,2 60,4 302

На рис. 96 представлено распределение насыщенности для двух моментов времени.