XIII. Неустановившаяся фильтрация газа

 

Дифференциальное уравнение неустановившейся изотерми­ческой фильтрации идеального газа по закону Дарси имеет вид

(XIII.1)

или

(XIII.2)

Это уравнение является нелинейным уравнением параболи­ческого типа, оно отличается от дифференциального уравнения упругого режима тем, что искомой функцией является не дав­ление р, а квадрат давления р², а вместо постоянного коэффи­циента пьезопроводности х в уравнение входит переменная вели­чина kp/mx.

Точные решения нелинейного уравнения (XIII.2) получены только для некоторых частных задач. Как правило, это урав­нение интегрируется приближенными методами.

Наиболее простым приближенным методом является метод линеаризации, предложенный И. А. Чарным, в котором переменное значение коэффициента kp/mµ заменяется усредненным значением kp_ср/mµ, где

здесь р_max и р_min — максимальное и минимальное давления в залежи за расчетный период, или

При такой замене уравнение (XIII.2) приводится к линей­ному дифференциальному уравнению теплопроводности. Это дает возможность нестационарное движение газа рассчитывать жак движение упругой жидкости по формулам упругого ре­жима фильтрации.

Л. С. Лейбензоном было лолучено решение задачи об истечении газа из полосообразного замкнутого пласта при условии постоянного давления на галерее (рис. 81). Задача сводится к интегрирова­нию дифференциального уравнения

(XIII.3)

при начальном и граничных условиях:

при t =0

при x =0

при x=l (XIII.4)

— условие на непроницаемой границе газового пласта.

Задача решалась методом последовательных приближений.

В первом приближении коэффициент, входящий в правую часть (XIII.3), считается постоянным и равным .

При этом (XIII.3) обращается в уравнение теплопроводно­сти, интеграл которого при условиях (XII 1.4) имеет вид

(XIII.5)

Во втором приближении принимается, что переменное дав­ление p, входящее в коэффициент kp/mµ, зависит только от времени t и выражается формулой

(XIII.6)

далее, введя новую переменную

(XIII.7)

приведем (XIII.3) к уравнению теплопроводности

(XIII.8)

решение которого при условиях (XIII.4) дается уравнением (XIII.5), в котором переменная t должна быть заменена на θ:

(XIII.9)

Объемный дебит галереи, приведенный к атмосферному дав­лению, можно записать в виде

(XIII.10)

Многие задачи неустановившейся фильтрации газа решаются «приближенно по методу последовательной смены стационарных состояний с привлечением уравнения материального баланса газа.

Если газовая залежь замкнута, то отобранное за время dt количество газа по объему, приведенному к атмосферному дав­лению и пластовой температуре, равное , равно изменению запасов газа в пласте за тот же промежуток времени.

Если объем порового пространства Ω постоянный, газ идеаль­ный, а фильтрация изотермическая, то изменение запасов можно представить в виде , где dp — изменение средневзвешенного по объему давления в газовой залежи за промежуток dt. Урав­нение

(XIII.11)

называется дифференциальным уравнением истощения газовой залежи.

При неустановившейся плоскорадиальной фильтрации газа средневзвешенное давление 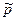мало отличается от контурного, поэтому, заменяя 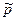на p_k записывают уравнение истощения газовой залежи в виде

(XIII.12)

Уравнение (XIII. 12) в сочетании с методом последователь­ной смены стационарных состояний позволяет определять рас­пределение давления по пласту, изменение давления с течением времени в любой точке пласта, изменение во времени дебитов таза при эксплуатации залежи с различными условиями на забое. Такими простейшими условиями являются следующие:..a) Q_aт = const; б) p_c = const; в) , где c = 2nr_chw_max, a w_max — максимально допустимая скорость фильтрации газа, ис­ключающая возможность выноса песка и образования песчаных пробок.

 

Задача 118

 

Определить падение давления р_к на внешней границе полосообразной газовой залежи длиной l = 7500 м, шириной В = 800 м, мощностью h = 10 м (см. рис. 81), если коэффициент пористости пласта m = 20%, коэффициент проницаемости k = 0,5 Д, коэф­фициент вязкости µ = 0,014 мПа•с, начальное пластовое давле­ние р_н = 14, 7 МПа (150 кгс/см²). Давление на выходе газа в галерею постоянно и равно р_г = 12,74 МПа (130 кгс/см²).

Найти также приведенный к атмосферному давлению и пла­стовой температуре расход газа Q_ат и распределение давления по длине пласта через t = 30 сут после начала отбора газа из галереи.

Решение. Для определения падения давления во времени на границе пласта р_к(t) и распределения давления по длине пла­ста р(х) в момент t = 30 сут используем решение Л. С. Лейбеизона по методу последовательных приближений (XIII.9).

Прежде всего подсчитаем значение параметра

и значения переменной Q(t) в разные моменты

 

а результаты поместим в табл. 19.

 

 

 

По формуле Л. С. Лейбензона на границе пласта (при x=l) имеем

 

Значения величин, входящих в эту формулу, приведены в табл. 19.

На рис. 82 представлен график зависимости р_к(t).

Закон распределения давления по пласту через 30 сут = 2,59•10⁶ с после начала отбора:

Результаты расчетов даны в табл. 20. На рис. 83 показана кривая изменения давления по пласту.

 

 

 

Расход газа, приведенный к атмосферному давлению и пла­стовой температуре, найдем по (XIII.10).

 

Задача 119

 

Газовая скважина расположена в центре кругового замкну­того пласта радиусом R_к =1000 м, мощностью h = 8 м и эксллуатируется при постоянном давлении на забое p_c = 6,86 МПа (70 кгс/см²)..Начальное давление в газовой залежи р_н = 11,76 МПа (120 кгс/см²), коэффициент проницаемости пласта k = 800 мД, коэффициент пористости пласта m =18%, динами­ческий коэффициент вязкости газа µ = 0,013 мПа•с, радиус скважины r_с = 10 см.

Найти изменение во времени давления на внешней границе залежи p_k(t) и приведенного объемного дебита скважины.

Решение. Полагая, что средневзвешенное пластовое давление газа 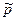равно давлению на внешнем контуре р_к, решим задачу методом последовательной смены стационарных состояний. За время dt при изотермическом процессе из залежи отбирается количество газа (по объему, приведенному к атмосферному давлению)

(XIII.13)

Учитывая, что

(XIII.14)

и подставляя эти выражения в уравнение материального ба­ланса (XIII.13), получим

Интегрируя по t от 0 до t и по р_к от р_н до p_k, найдем

Подставляя исходные данные подсчитаем для различных р_к значения t:

или

Результаты подсчетов представлены на рис. 84 и ниже.

p_k, МПа …………..11,76 10,78 9,8 8,82 7,84 6,96

t, сут ………………0 3,77 8,88 16,5 30,5 80,5

Q_ат,м³/cут ……….13,4·10⁶10,1·10⁶7,2·10⁶4,51·10⁶2,11·10⁶ 1,99·10⁵

 

Подставляя найденные значения р_к в (XIII.14), найдем из­менение Qат во времени

Cоответствующие значения дебатов даны на рис. 85.

 

 

 

Задача 120

 

Определить время истощения газовой залежи и изменение во времени давления на внешней границе и на забое скважины, считая, что скважина дренирует круговую зону радиуса R_к = = 500 м и эксплуатируется с постоянным приведенным дебитом Qaт = 500 000 м³/сут. Начальное пластовое давление р_н = 9,8 МПа (100 кгс/см²), конечное давление на забое газовой скважины (Р_с)_кон = 0,101 МПа (1,033 кгс/см²), мощность пласта h =12 м, радиус скважины r_с =10 см, коэффициент проницаемости пласта k = 500 мД, коэффициент пористости m ==20%, динамический коэффициент вязкости газа µ = 0,015 мПа·с.

Решение. Из уравнения материального баланса, в котором средневзвешенное пластовое давление заменено контурным, имеем

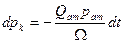(XIII.15)

Интегрируя (XIII. 15) по р_к в пределах от р_н до р_к и по t ют 0 до t получим

(XIII.16)

Из формулы дебита

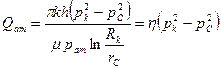
где

найдем давление на забое скважины

(XIII.17)

По значению забойного давления в конце разработки р_с.кон. найдем конечное значение давления на внешней границе р_{к.кон .}

Подставляя полученное зна­чение р_к.кон в (XIII.16), найдем время истощения газовой залежи:

 

Изменение во времени р_к и р_с определяется из (XIII.16) и (ХШ.17).

Результаты подсчетов приведены на рис. 86 и ниже.

t, сут..................... О 50 100 150 200 291

р_к, кгс/см²..............100 86,3 72,6 58,9 45,2 20,2

р _с, кгс/см²..............97,9 83,9 69,7 55,3 40,5 1,033

 

Задача 121

 

Определить изменение во времени дебита газовой скважины, давления на внешней непроницаемой границе р_к(t) и давления на забое скважины р_с(t) эксплуатирующейся при поддержании постоянной скорости движения газа в призабойной зоне пласта. Начальное пластовое давление р_н = 9,8 МПа (100 кгс/см²), ра­диус контура зоны дренирования R_k = 750 м, мощность пласта h =10 м, коэффициент проницаемости пласта k = 0,3 Д, коэффициент пористости пласта m = 20%, динамический коэффици­ент вязкости газа в пластовых условиях µ = 0,012 сП, радиус скважины r_с = 0,1 м. Коэффициент с, который соответствует максимально допустимой скорости фильтрации в призабойной зоне, определяемый практически, равен . Принять атмосферное давление р_ат = 0,098 МПа (1 кгс/см²).

Решение. Если газ отбирается при поддержании мак­симально допустимой скорости фильтрации w_max у забоя скважины, то приведенный дебит

(XIII.18)

обозначая

получим

(XIII.19)

С другой стороны,

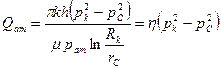(XIII.20)

Приравнивая соотношения (XIII.19) и (XIII.20), найдем

откуда

Обозначая , запишем

(XIII.21)

Подставляя (XIII.21) в (XIII.19), найдем зависимость дебита Q_ат от p_k

Из уравнения материального баланса, заменяя среднее пла­стовое давление контурным, найдем

(XIII.22)

Вводя новую переменную

и интегрируя дифференциальное уравнение (XI 11.22), получим

(XIII.23)

 

 

 

 

Подсчитаем объем норового пространства

значение коэффициентов

Подставляя численные значения параметров а_, с, р_ат и р_н в соотношение (XIII.23), задаваясь различными значениями р_к, определим значения t. Соответствующие значения p_c(t) и Q_ат{t) найдем из выражений (XIII.19) и (XIII.21). Результаты вы­числений представлены на рис. 87, 88 и ниже.

t, сут ………………0 226 462 776 1196 1825 3130 4250 6100

p_{k ,} МПа…………9,8 8,33 6,86 5,39 3,92 2,45 0,980 0,490 0,210

p_c, МПа…………9,62 8,15 6,68 5,22 3,74 2,28 0,822 0,345 0,098

Q_ат ·10^-5,м³/сут..2,66 2,25 1,85 1,445 1,035 0,632 0,227 0,0955 0,0271