Суперпозиция в задачах упругого режима

 

Метод суперпозиции (наложения фильтрационных потоков) широко применяется и в задачах неустановившихся течений при упругом режиме.

Если в пласте действует группа скважин, то понижение дав­ления в какой-либо точке пласта определяется сло­жением понижений давления, создаваемых в этой точке отдель­ными скважинами

(XII.18)

где п — число скважин; Q_j — дебит j -той скважины, причем Q_j > 0, если скважина эксплуатационная, и Q_j < 0, если сква­жина нагнетательная; r_j — расстояние от центра j -той сква­жины до точки, в которой определяется понижение давления.

Если скважины начали работать в разное время, то (XII.18) будет иметь вид

(XII.19)

где t_j —время, прошедшее с начала работы j -той скважины.

Методом суперпозиции можно решить задачи, связанные с пуском, остановкой или с изменением темпа добычи сква­жины. Пусть, например, скважина была пущена в эксплуатацию спостоянным дебитом Q и через промежуток времени Т оста­новлена. Требуется определить давление в любой точке пласта. Для решения задачи предположим, что скважина продолжает работать с тем же дебитом; тогда к моменту t после остановки понижение давления в какой-либо точке пласта, вызванное пус­ком непрерывно работающей скважины, будет равно

Допустим мысленно, что в том же месте, где расположена эксплуатационная скважина, в момент остановки начала рабо­тать нагнетательная скважина с тем же дебитом. К моменту t повышение давления в какой-либо точке пласта, вызванное пуском нагнетательной скважины, определится по формуле

Результирующее понижение давления ∆р запишется в виде

(XII.20)

Если аргументы функций малы, то можно использовать приближенную формулу (XII.9), и тогда

(XII.21)

Задача 107

 

Нефтяная залежь площадью S = 500 га и мощностью h = 30м имеет пористость m = 20% и водонасыщенность σ_в = 30%. Сколь­ко нефти можно отобрать за счет объемного упругого расшире­ния жидкости при падении давления от 300 кгс/см² (29,4 МПа) до 200 кгс/см² (19,6 МПа), если коэффициент сжимаемости нефти , а коэффициент сжимаемости воды β_в = 3,06·10^-10 м²/Н?

Пласт считать недеформируемым.

Решение. Считая нефть и воду упругими жидкостями, опреде­лим изменение объемов, занимаемых нефтью и водой при паде­нии давления на ∆р =100 кгс/см² (9,8 МПа):

объем вытесненной нефти равен сумме объемов

 

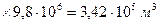
Задача 108

 

Определить упругий запас нефти в замкнутой области нефте­носности площадью 4500 га, мощностью h =15 м, если средне­взвешенное пластовое давление изменилось на 50 кгс/см², пористость пласта m =18%, коэффициент сжимаемости нефти β_H = 2,04·10^-9 м²/Н, насыщенность пласта связанной водой σ_в = 20%, коэффициент сжимаемости воды β_в = 4,59·10^-10м²/Н, коэффициент сжимаемости породы β_с = 1,02·10^-10 м²/Н.

Ответ: = 1,35·10⁶ м³.

 

Задача 109

 

Определить количество нефти, полученное за счет упругого расширения нефти, воды и горной породы, если площадь об­ласти нефтеносности S_H = 1000га, законтурная вода занимает площадь S_В = 10 000 га, средняя мощность пласта h = 10м, пористость пласта m = 25%, водонасыщенность в зоне нефтенос­ности σ_В =2О%, коэффициенты сжимаемости нефти, воды и по­роды соответственно равны

Пластовое давление снижается от 180 до 80 кгс/см².

Решение. Коэффициент нефтеотдачи за счет упругого рас­ширения определяется как отношение объема нефти, получен­ного за счет сжимаемости, к первоначальному объему нефти

Начальный объем нефти

Объем нефти, вытесняемой из зоны нефтеносности при паде­нии давления на ∆р = 100 кгс/см² за счет сжимаемости нефти и пористой среды, равен

где

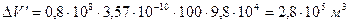
За счет расширения воды и породы в зоне нефтеносности объем вытесненной нефти составит

где

Объем нефти, вытесняемой из окружающей зоны водонос­ности за счет упругости воды и пласта, равен

 

Задача 110

 

Определить дебит галереи, расположенной в полосообразном полубесконечном пласте (см. рис. 74) шириной B = 300 м, мощ­ностью h =15м, с коэффициентом проницаемости k = 0,8 Д, в момент t = 2 сут с начала эксплуатации с постоянным забой­ным давлением р_г = 9,8 МПа. Начальное пластовое давление р_к = 12,74 МПа, коэффициент сжимаемости жидкости и породыравен соответственно р_ж = 1,53·10⁹ м²/Н и р_с = 0_э612·10^-10 м²/Н, коэффициент пористости m = 20%, динамический коэффициент вязкости нефти μ= 1,5 мПа·с.

В пласте имеет место неустановившаяся фильтрация упру­гой жидкости по закону Дарси.

Найти дебиты по точной формуле и по формуле, получен­ной по методу последовательной смены стационарных со­стояний.

Решение. Распределение давления в пласте при неустановив­шейся параллельно-струйной фильтрации упругой жидкости к прямолинейной галерее при постоянном давлении на забое выражается следующей формулой (точное решение):

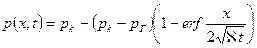
где

— интеграл вероятностей.

Согласно закону Дарси

Найдем :

поэтому

 

Коэффициент пьезопроводности א в условиях рассматривае­мой задачи равен

Дебит, определенный по точной формуле, будет

По методу последовательной смены стационарных состоянии дебит приближенно определяется по формуле для стационар­ного режима движения

где l{t) —длина, на которую распространилось бы понижение давления к моменту t, если бы давление в зоне депрессии меня­лось по прямой линии; l(t) определяется из условия матери­ального баланса при p_Г = const и равна

Тогда

Погрешность при определении дебита по приближенной формуле составит

 

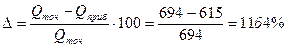
Задача 111

 

Представить графически изменение во времени давления на забое галереи, проведенной в полосообразном полубесконечном пласте (см. рис. 74), если в момент t = 0 ее начали эксплуати­ровать с постоянным дебитом Q = 500 м³/сут. Ширина галереи В = 400 м, мощность пласта h = 18 м, коэффициент проницае­мости k = 0,5 Д, коэффициенты сжимаемости жидкости β_ж =2,04·10^-9 породы β_с = 0,51·10^-10 м²/Н, коэффициент пористости m = 16%, коэффициент вязкостн жидкости μ = 3 мПа·с, начальное пластовое давление р_k =14,7 МПа.

В пласте имеет место неустановившаяся фильтрация упругой жидкости по закону Дарси.

Сравнить значение депрессии в момент t =10 сут, определен­ное по точной формуле, с депрессией, найденной по методу последовательной смены стационарных состояний.

Решение. В рассматриваемом случае дифференциальное уравнение фильтрации упругой жидкости в деформируемой по­ристой среде имеет вид

(XII.22)

а начальное и граничные условия запишутся следующим об­разом:

при t = 0 p (x,0) = p_k

(XII.23)

при x=0

(XII.24)

Умножая (XII.22) на , дифференцируя по х и учитывая, что получим

или, изменяя порядок дифференцирования,

т.е.

(XII.25)

Уравнение теплопроводности (XII.25) совпадает с уравне­нием (XII.22), и начальным и граничным условиями являются:

при t = 0 w(x, 0) = 0 (XII.26)

при х = 0 w (0, t) = w₁ = const. (XII.27)

 

Решением уравнения (XII.25) при условиях (XII.26) и (XII.27) является интеграл вероятности

(XII.28)

Для того, чтобы найти закон изменения давления, необхо­димо проинтегрировать по х уравнение

при фиксированном t:

(XII.29)

Возьмем по частям интеграл

Обозначим

 

тогда

(XII.30)

Подставив (XII.30) в (XII.29), получим

где

Устремляя и учитывая, что при этом ,

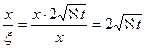
найдем депрессию в любой момент времении

давление па забое галереи

Подсчитаем коэффициент пьезопроводностии

постоянную величину

Тогда

, МПа

Задаваясь различными , найдем и результаты поместим в табл.15.

График зависимости от приведен на рис. 76.

Определим депрессию по методу последовательной смены стационарных состояний через сут после начала отбора. Согласно этому методу депрессия находится по формуле дебита галереи при установившейся фильтрации по закону Дарси, а под l(t) понимается длина возмущенной области, которая при постоянном отборе равна

 

 

 

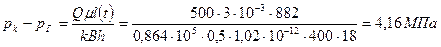
Соответствующая депрессия, определенная по точной фор­муле (см. табл. 15), равна

Погрешность

 

Задача 112

 

Найти распределение давления в полосообразном полубес­конечном пласте в момент t ==15 сут с начала отбора, если в пласте имеет место приток упругой жидкости к дренажной галерее при условии постоянного отбора Q = 100 м³/сут; длина галереи В = 250 м; мощность пласта h == 10 м, коэффициент про­ницаемости k = 400 мД, коэффициент сжимаемости пористой среды р_с = 0,306 • 10^-10 м²/Н, коэффициент сжимаемости жидко­сти β_ж = 4,59·10^-10 м²/Н, динамический коэффициент вязкости μ = l,2 мПа·с, коэффициент пористости m =l5%, начальное пластовое давление р_к = 11,76 МПа (120 кгс/см²).

Задачу решить по точной формуле, по методу последова­тельной смены стационарных состояний и по методу А. М. Пирвердяна

Решение. В задаче 111 выведена точная формула для раз­ности давлений

(XII.31)

где

Из этой формулы давление на забое галереи равно

(XII.32)

Подставив (XII.32) в (XII.31), получим

(XII.33)

Вычислим постоянные множители:

при этом .

Задаваясь различными х, подсчитаем р{х) при t =15 сут. Результаты расчетов по точной формуле (XII.33) приведены в табл. 16 и представлены на рис. 77 (кривая 1).

 

 

По приближенному методу А. М. Пирвердяна при постоян­ном отборе

(XII.34)

где

При заданном t =15 сут

(XII.35)

Результаты вычислений по (XII.35) приведены в табл. 17 и,на рис. 77 (кривая 2).

По методу последовательной смены стационарных состояний давление распределяется линейно

(XII.36)

где

давление на забое галереи

Следовательно,

(XII.37)

Прямая 3, соответствующая уравнению (XII.37), изображена на рис. 77.

Как видно из полученных результатов, распределение дав­ления по методу Пирвердяна ближе к истинному, чем распре­деление давления по методу последовательной смены стацио­нарных состояний.

 

Задача 113

 

Из скважины, расположенной в бесконечном пласте, начали отбор нефти, поддерживая постоянное давление на забое р_с = 8,82 МПа. Начальное пластовое давление p_k= 11,76 МПа. Используя метод последовательной смены стационарных состоя­ний, определить дебит скважины через 1 ч, 1 сут и 1мес после начала эксплуатации, если коэффициент проницаемости пласта k = 250 мД, мощность пласта h = 12 м, коэффициент пьезопровод-пости пласта א = 1,5 м²/с, коэффициент вязкости нефти μ =l,3 сП. Скважина гидродинамически совершенная, радиус ее r_с = 0,1 м.

Указание. По методу последовательной смены стационарных состояний дебит скважины определяется по формуле Дюпюи, в которой под R_k понимается приведенный радиус влияния сква­жины, который увеличивается с течением времени по закону .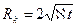

Ответ: Q_час = 515м³/сут; Q_cyт = 424 м³/сут; Q_мес = 356 м³/сут.

 

3адача 114

 

Определить коэффициент гидропроводности пласта икоэффициент пьезопроводности пласта א по данным об измене­нии давления на забое совершенной скважины, расположенной вбесконечном пласте постоянной мощности. Скважина работает с постоянным дебитом Q = 100 м³/сут в условиях упругого ре­жима. Начальное пластовое давление р_k =150 кгс/см², радиус скважины r_с = 0,1 м. Изменение депрессии с течением времени приведено ниже:

Номер ……………………..1 2 3 4 5

t............................................15 мин 1 ч 12 ч 1 сут 5 сут

………………………….3,46 3,84 4,57 4,76 5,23

Решение. Изменение давления на забое скважины опреде­ляется по формуле

По приведенным выше дан­ным построим график зависимо­сти от (рис. 78).

Как видно из рис. 78, зави­симость от 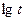линейная:

Это дает возможность опре­делить свободный член по отрез­ку, отсекаемому прямой на оси ординат, и коэффициент при 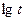по тангенсу угла наклона пря­мой к оси .

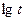Из графика следует, что b = 1,5 кгс/см²,

 

Из первой формулы следует, что

откуда коэффициент гидропроводности пласта

а

откуда

 

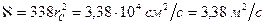
Задача 115

 

Гидродинамически совершенная скважина, расположенная в центре кругового пласта радиуса R_k=10 км с горизонтальными и непроницаемыми кровлей и подошвой, до момента остановки работала в течение такого продолжительного периода, что распределение давления в пласте можно принять за установив­шееся. Дебит скважины до остановки Q = 120 м³/сут, динами­ческий коэффициент вязкости μ = 2 сП, коэффициент проницае­мости пласта k = 600 мД, мощность пласта h = 10 м, радиус сква­жины r_с = 0,1 м, коэффициент пьезопроводности пласта א = 2,5 м²/с Найти по методу суперпозиции нарастание давления на забое скважины, принимая p_k = 14,7 МПа (150 кгс/см²).

Решение. Установившуюся депрессию , пред­шествующую остановке скважины, определим по формуле Дюпюи

По методу суперпозиции считаем, что с момента остановки скважины в той же точке пласта начала работать одновременно с эксплуатационной скважиной нагнетательная скважина, имею­щая тот же дебит. При этом результирующий дебит равен ну­лю, а разность давлений

где — повышение давления на забое, вызван­ное работой только нагнетательной скважины, которое опреде­ляется формулой

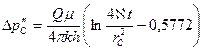
Таким образом,

откуда

 

Задача 116

 

Определить коэффициент гидропроводности пласта ,если известно, что гидродинамически совершенная скважина., расположенная в центре кругового пласта радиуса R_k, длитель­ное время эксплуатировалась с постоянным дебитом Q = 80 м³/сут, затем дебит скважины мгновенно уменьшился до Q₁ = 55 м³/сут. В последующее время эксплуатации скважины дебит Q_i сохранялся неизменным.

Изменение давления на забое скважины во времени пред­ставлено ниже. Время t = 0 соответствует моменту изменения-дебита скважины.

Номер ……………….1 2 3 4 5 6

t ……………………...5 мин 15 мин 3 ч 1 сут 3 сут 10 сут

3,71 3,62 3,44 3,27 3,18 3,1

…………………..2,48 2,95 4,03 4,94 5,41 5,94

Решение. По принципу суперпозиции понижение давления на забое скважины найдем по формуле

где первое слагаемое определяет депрессию, вызванную дли­тельной эксплуатацией скважины с дебитом Q, а второе слагае­мое—повышение давления за счет действия в той же точке пласта нагнетательной скважины с дебитом (Q — Q₁).

Представляя приближенно интегральную показательную функцию через логарифм, получим

Выделяя слагаемое, содержащее , запишем

Из последней формулы видно, что зависимость ∆р_с от lg t прямолинейная с угловым коэффициентом

 

По приведенным выше данным построим график в координа­тах ∆ р_с — lg t и определим значение i (рис. 79).

По полученному значению i найдем коэффициент гидропроводноети

 

Задача 117

 

Гидродинамическая совер­шенная скважина радиусом r_C = 10 см начала работать в бес­конечном пласте с постоянным дебитом Q =80 м³/сут. Мощность пласта h = 7,5 м, коэффициент проницаемости k = 400 мД, коэф­фициент пьезопроводности א = 2 м²/с, динамический коэффи­циент вязкости жидкости μ = 1,5·10^-3 Па·с. По истечении T =10 сут скважина была мгно­венно остановлена. Определить: 1) распределение давления в пласте в моменты t₁ =l сут и t₂ =5 сут после остановки скважины; 2) радиус зон, в которых с точностью до 1% давление в моменты и будет посто­янным.

Решение. Используя метод суперпозиции, найдем результи­рующее понижение давления в любой точке пласта

(XII.38)

считая, что в некоторый момент времени пущена в эксплуата­цию скважина с постоянным дебитом, а через промежуток вре­мени Т в этой же точке пласта начала работать нагнетательная скважина с тем же дебитом. Время Т соответствует моменту мгновенной остановки эксплуатационной скважины, начиная с этого момента отбор жидкости из пласта равен нулю.

— понижение давления, вызванное действием эксплуата­ционной скважины, определяемое по формуле

(XII.39)

—повышение давления, вызванное действием нагнетательной сважины,

(XII.40)

Учитывая выражения (XII.39) и. (XII.40), получим

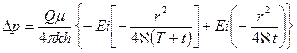(XII.41)

Известно, что при малых значениях аргумента функцию можно приближенно представить в виде

Погрешность не превышает 1%, если

или (XII.42)

 

 

Поэтому (XII.41) можно записать в виде

(XII.43)

 

при выполнении условия (XII.42).

Как следует из (XII.43), в некоторой области пласта, опре­деляемой условием (XII.42), для одного и того же момента времени давление будет одинаково.

При t₁ = 1 сут эта зона ограничена радиусом

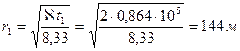
при t₂ = 5 сут

Понижения давления в этих зонах соответственно равны

Вне указанных зон понижение давления надо определять по точной формуле (XII.41). Результаты расчетов ∆р помещены в табл. 18 и представлены на рис. 80.