Прогнозирование траектории цели выполняется на основе метода экстраполяции.
Содержание задачи экстраполяции движения цели состоит в следующем. На основе информации о движении цели до отделения НАСП от БАК продолжить (экстраполировать) движение цели на некотором интервале времени после отделения. В частности, этот интервал может быть равным времени полета T НАСП от момента отделения до встречи с целью. Говоря о движении цели, здесь имеется в виду закон ее движения.
Пусть движение цели относительно воздуха характеризуется вектором 
, определяемым относительно некоторого начала O, жестко связанного с воздухом. Годограф вектора 
соответствует траектории цели (рис. 12).
Для момента отделения НАСП 
. Далее траектория цели экстраполирована – на рис. 12 показана пунктиром. На участке экстраполяции траектория определяется вектором 
. При t = T вектор 
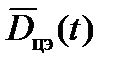принимает значение 
, т.е. определяет положение упрежденной точки относительно начала 
.
Из рассмотрения схемы на рис. 12 следует:
. (15)
Таким образом, если удалось экстраполировать движение цели и известно время T, может быть определен вектор 
.
Один из возможных вариантов экстраполяции движения цели, определения вектора 
, основан на известном в высшей математике методе разложения функций в ряд для приближенного их представления.
Имея в виду экстраполяцию движения наземной цели, можно предполагать, что в малой окрестности относительно точки траектории цели в t = 0 ее можно считать гладкой кривой. Тогда можно воспользоваться, например, простейшим степенным рядом Тэйлора-Макларена для приближенного представления функции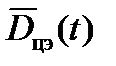 
.
Этот ряд можно записать в таком виде:
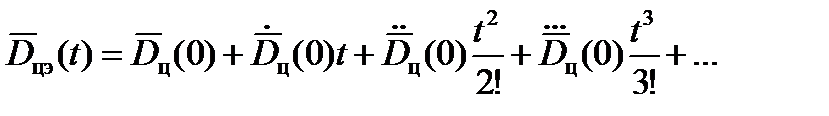(16)
Значения 
и производных по времени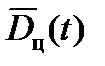 
к моменту отделения НАСП в (16) должны быть определены на основе наблюдения за движением цели до отделения НАСП.
Формулу (16) можно записать в другом виде, применив привычные обозначения
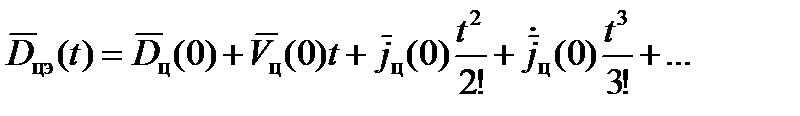, (17)
где 
– вектор скорости цели в момент отделения НАСП;
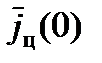– вектор ускорения цели в момент отделения НАСП;
– производная от вектора ускорения по времени в момент отделения НАСП.
Анализируя выражения (16) и (17), можно заметить следующее:
- точность представления 
степенным рядом определяется точностью измерения 
, порядком учтенных в ряду производных и точностью их определения;
- чем на большее время требуется экстраполировать движение цели, тем точнее необходимо представлять функцию 
;
- необходимость в учете производных от 
того или иного порядка определяется видом траектории цели.
Экстраполируя траекторию рядом (17), мы воспользовались для представления 
лишь значениями некоторых фазовых координат цели для t = 0.Другими словами, при экстраполяции не учитывали в деталях характер изменения 
, т.е. предысторию процесса движения цели.
Имея в виду выражение (15) для 
, следует заметить, что точность определения 
при заданном T будет зависеть от точности, с которой будут определены 
, 
, 
и т.д.
На практике для получения значений указанных векторов используются соответствующие бортовые датчики информации. Датчики осуществляют измерения с ошибками, поэтому в целях повышения точности определения 
должна быть применена фильтрация необходимых фазовых координат цели. Осуществление фильтрации потребует учета предыстории движения цели на том или ином промежутке времени до отделения НАСП.
Если для экстраполяции движения цели принято выражение (17), то можно определить 
по другой формуле, вместо (16)
.
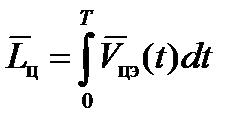В соответствии с (17):
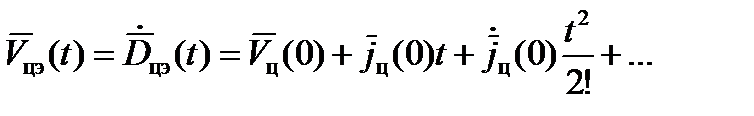
Подставив это выражение в формулу для 
, получим:
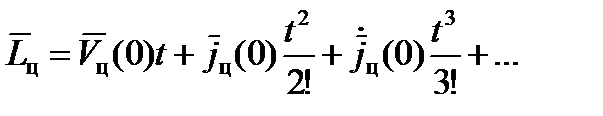
Возможен другой вариант постановки и решения задачи экстраполяции движения цели, когда наряду с продолжением движения обеспечивается и фильтрация ошибок в определении вектора 
.
Представим вектор 
с учетом ошибок наблюдений в виде матрицы-столбца, например, в стабилизированной системе координат O:
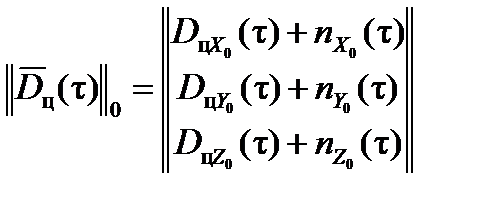, (18)
где 
, 
, 
– ошибки наблюдений за движением цели – случайные функции времени.
В (18) через 
обозначен интервал времени, предшествующий моменту отделения НАСП.
Задача состоит в определении такого оператора фильтрации ошибок наблюдений и экстраполяции (упреждения), который бы наилучшим, в известном смысле, образом обеспечивал определение 
, где 
есть время упреждения.
Идеальный оператор 
обеспечивает следующее преобразование вектора (18):
.
Здесь, как мы видим, используются прошлые данные о процессе движения цели с учетом возможных ошибок в получении этих данных.
Реально следует назвать наилучшим тот оператор 
, который минимизирует среднее значение выбранной соответствующим образом функции от ошибки 
экстраполированной, например, проекции 
:
.
Можно, в частности, в качестве указанной функции рассматривать квадрат ошибки 
. По аналогии можно записать такие же выражения для других проекций 
.
Постановка и решение указанной задачи по определению оператора фильтрации и упреждения принадлежат Н. Винеру. Решение было выполнено им для случая, когда сигнал 
и шум (ошибка 
) являются стационарными случайными функциями, и оператор выбирался с учетом указанного выше критерия – минимума среднего квадрата ошибки.
Дальнейшее развитие теории определения оптимальных операторов фильтрации и упреждения применительно к экстраполяции движения воздушной цели принадлежит В.М. Семенову.
Возможен еще один подход к решению задачи фильтрации. Это статистический метод фильтрации экстраполяции координат цели. Рассмотрим его в постановке Б.В. Воронова.
Пусть над координатой цели 
осуществлено N наблюдений. Причем, каждый раз координата представляется степенным рядом вида:
, (19)
где 
, являются многочленами степени 
.
Применение максимума правдоподобия при условии независимости результатов измерений между собой и наличии нормального закона ошибок измерений приводит к задаче об определении оценок 
по методу наименьших квадратов. При этом применение ортогональных полиномов (полиномов П.Л. Чебышева) дает следующую формулу:
.
Для выполнения экстраполяции 
при выборе степени полинома n после определения по данным измерений 
коэффициентов 
, 
, …, 
можно по формуле (19) найти значени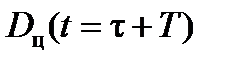е 
, где 
интервал измерений величины 
, а T – время полета НАСП, на которое экстраполируется координата 
.
