Для исследования движения ЛА как твердого тела применяются прямоугольные правые системы координат, определяющие его пространственное положение тремя линейными координатами и тремя углами. В зависимости от расположения начала системы отсчета выделяют две группы систем координат: связанные с землей и связанные с ЛА.
В первой группе наиболее часто используется инерциальная система координат Ox ин y ин z ин. Оси этой системы координат не изменяют своего направления в пространстве. Направление осей выбирают в соответствии с решаемой задачей. Инерциальная система координат участвует только в поступательном движении Земли вокруг Солнца, и положение ее осей не зависит от суточного вращения Земли.
Большая вторая группа координат объедена общим признаком – расположением начала координат в характерной точке движущегося ЛА, обычно в центре масс. В практике используют географическую, горизонтированную, траекторно-горизонтированную, связанную, скоростную и лучевую системы координат.
Географическая система координат Oxgygzg. Начало этой системы координат точка О совпадает с центром тяжести ЛА. Ось Охg лежит в меридиальной плоскости и направлена на север; ось Оуg направлена по нормали – географической местной (географической) вертикали – перпендикулярно оси Охg; ось Оzg вместе с осью Охg находится в местной горизонтальной плоскости и дополняет систему координат до правой тройки векторов.
Связанная система координат Ox св y св z св. Для определения координат БАК относительно географической системы координат применяется связанная с БАК система координат, то есть система, неподвижная относительно ЛА. Начало связанной системы координат совмещают с центром тяжести ЛА, который будем считать неподвижным относительно корпуса аппарата. Оси Ох св и Оу св располагают в плоскости симметрии ЛА, причем ось Ох св направляется вперед, а ось Оу св – вверх, перпендикулярно оси Ох св. Тогда ось Oz св, перпендикулярная к плоскости симметрии Ох св у св, образует правую систему координат и будет направлена в сторону правого крыла. Ось Ох св может быть направлена либо параллельно хорде крыла ЛА, либо вдоль строительной горизонтали. В данной задаче она направлена вдоль оси корпуса ЛА. Также полагаем, что связанные оси близки к главным центральным осям инерции ЛА.
БАК как жесткое тело имеет шесть степеней свободы, и соответственно положение БАК относительно географической системы координат определяется шестью координатами: тремя координатами x 0, y 0, z 0 начала О связанной системы координат и тремя углами между связанной и географической системами координат. Эти углы определяют следующим образом.
Углом рысканья ψ называют угол между проекцией оси Ох св связанной системы координат на местную горизонтальную плоскость Oxgyg и осью Охg географической системы координат (направлением на север).
Углом тангажа ϑ называют угол между продольной осью Ох св и местной горизонтальной плоскостью.
Углом крена γ называют угол между местной вертикальной плоскостью, проходящей через продольную ось Ох св, и осью Оу св.
Горизонтированная система координат Оx гор y гор z гор. Начало этой системы координат точка совпадает с центром тяжести ЛА. Ось Ох гор направляется по оси симметрии БАК и располагается в местной горизонтальной плоскости. Оу гор располагают в плоскости симметрии БАК и направляют вверх, перпендикулярно оси Ох гор. Боковая ось Оz гор дополняет две названные оси до правой системы координат.
Легко видеть, что положение горизонтированной системы координат относительно связанной определяется описанными выше углами крена γ и тангажа ϑ, а относительно географической – углом рысканья ψ.
Скоростная система координат Ox ск y ск z ск. При изучении движения центра тяжести БАК удобно в качестве подвижной системы координат выбирать систему с осью Ох ск, направленной по вектору воздушной скорости 
центра тяжести ЛА. Начало координат такой системы располагается в центре тяжести ЛА, оси Oy ск и Oz ск лежат в плоскости, нормальной к вектору воздушной скорости 
. В динамике полета направление оси Оу ск выбирают как правило в плоскости симметрии БАК (иногда в вертикальной плоскости Охgуg – полускоростная система координат). Боковая ось Oz ск, перпендикулярная этой плоскости симметрии, очевидно, будет направлена в сторону правого горизонтального крыла.
Положение скоростной относительно связанной системы координат определяется с помощью следующих углов.
Углом атаки α называют угол между проекцией вектора воздушной скорости 
на плоскость симметрии БАК и осью Ох св связанной системы координат;
Углом скольжения β называют угол между вектором воздушной скорости 
и плоскостью симметрии ЛА.
Траекторно-горизонтированная система координат Ox трг y трг z трг. Начало этой системы координат помещают в центр масс ЛА. Ось Ox трг располагают в местной горизонтально плоскости и направляют по вектору путевой скорости 
ЛА. Ось Oy трг направляют вверх от поверхности Земли в вертикальной плоскости, проходящей через ось Ox трг. Ось Oz трг направлена горизонтально в сторону правого крыла.
Положение траекторно-горизонтированной системы координат относительно географической определяется углом Y.
Путевым углом Y или углом курса называется угол между проекцией вектора земной скорости 
на горизонтальную плоскость и осью Охg.
В случае просто траекторной системы координат дополнительно необходимо учитывать угол q. Углом наклона траектории q называется угол между путевой скоростью БАК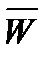 
и горизонтальной плоскостью.
Лучевая система координат Ox л y л z л. Она определена относительно связанной системы координат углами j y и j z, представляющими собой углы визирования цели, определяющие пространственное положение осей Oy л и Oz л лучевой системы координат относительно соответствующих осей связанной системы координат.
Положение лучевой системы координат относительно горизонтированной определяется помимо углов j y и j z углами крена γ и тангажа ϑ, которые были определены выше.
Преобразования, связанные с переходом из одной системы координат к другой, осуществляются с помощью матриц направляющих косинусов. Матрицу удобно обозначать двумя индексами 
, где нижний индекс соответствует основной системе координат, а верхний – системе, определяемой последовательным поворотом на эйлеровы углы относительно основной. Элементами матрицы, являются функции эйлеровых углов поворота:
.
Каждый элемент матрицы равен проекции единичного вектора, направленного по одной координатной оси основной системы, на соответствующую ось определяемой системы, то есть 
.
Функции углов записаны в каждом элементе в порядке, соответствующем очередности поворотов основной системы координат. Так, например, элемент 
означает, что сначала основную систему повернули на угол y, затем на угол J и в конце – на угол g.
Если надо осуществить переход от второй системы координат к первой, то необходимо воспользоваться транспонированной матрицей. Сложный последовательный переход от первой системы координат ко второй и от второй к третьей осуществляется по правилу перемножения матриц:
.
Матрица направляющих косинусов перехода от географической системы координат к связанной имеет следующий вид:
Матрица перехода от скоростной системы координат к связанной:
.
Матрица перехода от горизонтированной системы координат к связанной:
.
Матрица перехода от географической системы координат к горизонтированной:
.
Матрица перехода от лучевой к связанной системе координат:
.
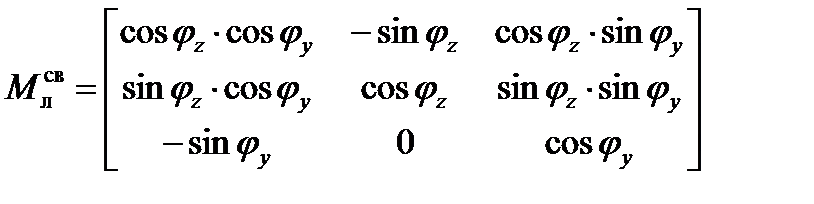Матрица перехода от лучевой к горизонтированной системе координат:
= 
= 
= 
= 
= 
= 
= 
= 
= 
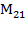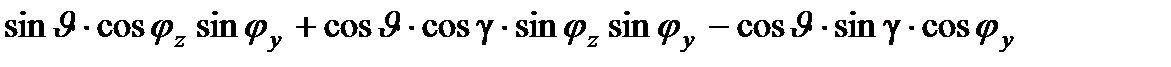
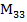При описании математической модели движения НАСП кроме указанных выше используются также следующие системы координат:
- установочная система координат НАСП Оx уст y уст z уст;
- связанная с осями НАСП система координат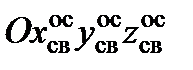 
.
Матрица перехода 
из установочной системы координат Оx уст y уст z уст в связанную с БАК О x св y св z св имеет вид:
,
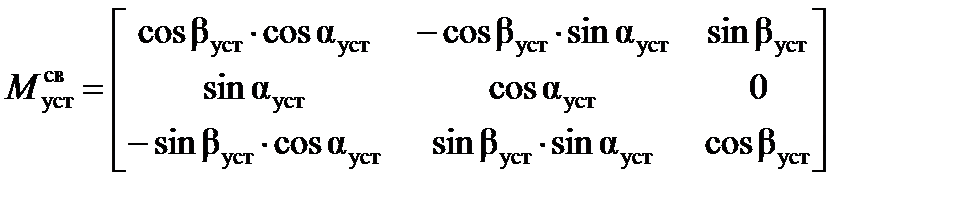где βуст – угол разворота НАСП относительно осей ЛА;
αуст – угол возвышения НАСП относительно осей ЛА.
Матрица перехода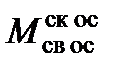 
из связанной с осями НАСП системы координат 
в полускоростную 
имеет вид:
,
где 
– угол атаки НАСП;
– угол скольжения НАСП.
