Інтервальний статистичний розподіл

h	x 1 – x 2	x 2 – x 3	x 3 – x 4	…	xk –1 – xk
ni	n 1	n 2	n 3	…	Nk
Wi	W 1	W 2	W 3	…	Wk

Перелік часткових інтервалів і відповідних їм частот, або відносних частот, називають інтервальним статистичним розподілом вибірки.

У табличній формі цей розподіл має такий вигляд:Тут h = x_i – x_{i –1} є довжиною часткового i -го інтервалу. Як правило, цей інтервал береться однаковим.

Інтервальний статистичний розподіл вибірки можна подати графічно у вигляді гістограми частот або відносних частот, а також, як і для дискретного статистичного розподілу, емпіричною функцією F ^*(x) (комулятою).

46) Полігон частот і відносних частот. Дискретний статистичний розподіл вибірки можна зобразити графічно у вигляді ламаної лінії, відрізки якої сполучають координати точок (x_i; n_i), або (x_i; W_i).

У першому випадку ламану лінію називають полігоном частот, у другому — полігоном відносних частот.

 

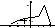
Гістограма частот та відносних частот. Гістограма частот являє собою фігуру, яка складається з прямокутників, кожний з яких має основу h і висотy .

Гістограма відносних частот є фігурою, що складається з прямокутників, кожний з яких має основу завдовжки h і висоту, що дорівнює .

Площа гістограми частот

Площа гістограми відносних частот .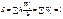

 

 

47) Числові характеристики:

вибіркова середня величина . Величину, яка визначається формулою

називають вибірковою середньою величиною дискретного статистичного розподілу вибірки.

Тут x_i — варіанта варіаційного ряду вибірки;

n_i — частота цієї варіанти;

n — обсяг вибірки ().

Якщо всі варіанти з’являються у вибірці лише по одному разу, тобто n_i =1, то

2) дисперсія. Для вимірювання розсіювання варіант вибірки відносно вибирається дисперсія.

Дисперсія вибірки — це середнє арифметичне квадратів відхилень варіант відносно , яке обчислюється за формулою

або

3) середнє квадратичне відхилення вибірки s_B. При обчисленні D _B відхилення підноситься до квадрата, а отже, змінюється одиниця виміру ознаки Х, тому на основі дисперсії вводиться середнє квадратичне відхилення

яке вимірює розсіювання варіант вибірки відносно , але в тих самих одиницях, в яких вимірюється ознака Х;

4) мода (Mo^*). Модою дискретного статистичного розподілу вибірки називають варіанту, що має найбільшу частоту появи.

Мод може бути кілька. Коли дискретний статистичний розподіл має одну моду, то він називається одномодальним, коли має дві моди — двомодальним і т. д.;

5) медіана (Me^*). Медіаною дискретного статистичного розподілу вибірки називають варіанту, яка поділяє варіаційний ряд на дві частини, рівні за кількістю варіант;

48) Визначення статистичної оцінки Інформація, яку дістали на основі обробки вибірки про ознаку генеральної сукупності, завжди міститиме певні похибки, оскільки вибірка становить лише незначну частину від неї (n < N), тобто обсяг вибірки значно менший від обсягу генеральної сукупності.Тому слід організувати вибірку так, щоб ця інформація була найбільш повною (вибірка має бути репрезентативною) і забезпечувала з найбільшим ступенем довіри про параметри генеральної сукупності або закон розподілу її ознаки. Параметри генеральної сукупності M(x_i)=X_г, D_г, δ_г, Mo, r_xy є величинами сталими, але їх числове значення невідоме. Ці параметри оцінюються параметрами вибірки: 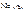які дістають при обробці вибірки. Вони є величинами непередбачуваними, тобто випадковими.

Тут через θ позначено оцінювальний параметр генеральної сукупності, а через — його статистичну оцінку, яку називають ще статистикою. При цьому θ = const, а — випадкова величина, що має певний закон розподілу ймовірностей. Зауважимо, що до реалізації вибірки кожну її варіанту розглядають як випадкову величину, що має закон розподілу ймовірностей ознаки гене­ральної сукупності з відповідними числовими характеристиками:M(x_i)=X_г=M(x), D(x_i)=D_г, δ(x_i)=δ_г

49) Точкові та інтервальні статистичні оцінки Статистична оцінка яка визначається одним числом, точкою, називається точковою. Беручи до уваги, що 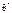є випадковою величиною, точкова статистична оцінка може бути зміщеною і незміщеною: коли математичне сподівання цієї оцінки точно дорівнює оцінювальному параметру θ, а саме: (1) то називається незміщеною; в противному разі, тобто коли точкова статистична оцінка називається зміщеною відносно параметра генеральної сукупності θ. Різниця (3) називається зміщенням статистичної оцінки Оцінювальний параметр може мати кілька точкових незміщених статистичних оцінок Точкова статистична оцінка називається ефективною, коли при заданому обсязі вибірки вона має мінімальну дисперсію. Отже, оцінка буде незміщеною й ефективною.

Точкова статистична оцінка називається ґрунтовною, якщо у разі необмеженого збільшення обсягу вибірки наближається до оцінювального параметра θ, а саме: Точкові статистичні оцінки є випадковими величинами, а тому наближена заміна θ на часто призводить до істотних похибок, особливо коли обсяг вибірки малий. У цьому разі застосовують інтервальні статистичні оцінки. Статистична оцінка, що визначається двома числами, кінцями інтервалів, називається інтервальною. Різниця між статистичною оцінкою 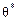та її оцінювальним параметром θ, взята за абсолютним значенням, називається точністю оцінки, а саме: (04) де δ є точністю оцінки. Оскільки є випадковою величиною, то і δ буде випадковою, тому нерівність (04) справджуватиметься з певною ймовірністю. Імовірність, з якою береться нерівність (04), тобто 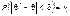, (05) називають надійністю. Рівність (05) можна записати так: . Інтервал ,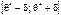

що покриває оцінюваний параметр θ ге­неральної сукупності з заданою надійністю g, називають довірчим.

51) Нульова та альтернативна статистичні гіпотези Гіпотезу, що підлягає перевірці, називають основною. Оскільки ця гіпотеза припускає відсутність систематичних розбіжностей (нульові розбіжності) між невідомим параметром генеральної сукупності і величиною, що одержана внаслідок обробки вибірки, то її називають нульовою гіпотезою і позначають Н ₀. Зміст нульової гіпотези записується так: 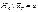; ; . Кожній нульовій гіпотезі можна протиставити кілька альтернативних (конкуруючих) гіпотез, які позначають символом Н _a, що заперечують твердження нульової. Так, наприклад, нульова гіпотеза стверджує: , а альтернативна гіпотеза — , тобто заперечує твердження нульової.

53) Статистичний критерій Для перевірки правильності висунутої статистичної гіпотези вибирають так званий статистичний критерій, керуючись яким відхиляють або не відхиляють нульову гіпотезу. Статистичний критерій, котрий умовно позначають через K, є випадковою величиною, закон розподілу ймовірностей якої нам заздалегідь відомий. Так, наприклад, для перевірки правильності 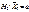як статистичний критерій K можна взяти випадкову величину, яку позначають через K = Z, що дорівнює і яка має нормований нормальний закон розподілу ймовірностей. При великих обсягах вибірки (n > 30) закони розподілу статистич­них критеріїв наближатимуться до нормального. Спостережуване значення критерію, який позначають через K ^*, обчислюють за результатом вибірки.

54) Критична область Множину W всіх можливих значень статистичного критерію K можна поділити на дві підмножини А і , які не перетинаються. 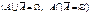. Сукупність значень статистичного критерію K Î А, за яких нульова гіпотеза не відхиляється, називають областю прийняття нульової гіпотези. Сукупність значень статистичного критерію K Î , за яких нульова гіпотеза не приймається, називають критичною областю. Отже, А — область прийняття Н ₀, — критична область, де Н ₀ відхиляється. Точку або кілька точок, що поділяють множину W на підмножини А і 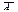, називають критичними і позначають через K _кр. Існують три види критичних областей: Якщо при K < K _крнульова гіпотеза відхиляється, то в цьому разі ми маємо лівобічну критичну область, яку умовно можна зобразити (рис. 1).

 

Якщо при нульова гіпотеза відхиляється, то в цьому разі маємо правобічну критичнуобласть

Якщо ж при і при нульова гіпотеза відхиляється, то маємо двобічну критичнуобласть.

Лівобічна і правобічна області визначаються однією критичною точкою, двобічна критична область — двома критичними точками, симетричними відносно нуля.

55) Перевірка правельності нульової гіпотези про нормальний закон розподілу ознаки генеральної сукупності Для перевірки правильності Н ₀ задається так званий рівень значущості a.

a — це мала ймовірність, якою наперед задаються. Вона може набувати значення a = 0,005; 0,01; 0,001. В основу перевірки Н ₀ покладено принцип , тобто ймовірність того, що статистичний критерій потрапляє в критичну область 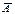, дорівнює малій імовірності a. Якщо ж виявиться, що 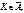а ця подія малоймовірна і все ж відбулася, то немає підстав приймати нульову гіпотезу. Пропонується такий алгоритм перевірки правильності Н ₀:

1. Сформулювати Н ₀ й одночасно альтернативну гіпотезу Н _a.

2. Вибрати статистичний критерій, який відповідав би сформульованій нульовій гіпотезі.

3. Залежно від змісту нульової та альтернативної гіпотез будується правобічна, лівобічна або двобічна критична область, а саме: нехай , тоді, якщо

, то вибирається правобічна критична область, якщо

, то вибирається лівобічна критична область і коли

, то вибирається двобічна критична область.

4. Для побудови критичної області (лівобічної, правобічної чи двобічної) необхідно знайти критичні точки. За вибраним статистичним критерієм та рівнем значущості a знаходяться критичні точки.

5. За результатами вибірки обчислюється спостережуване значення критерію .

6. Відхиляють чи приймають нульову гіпотезу на підставі таких міркувань: у разі, коли , а це є малоймовірною випадковою подією, і, незважаючи на це, вона відбулася, то в цьому разі Н ₀ відхиляється: для лівобічної критичної області 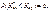; для правобічної критичної області

для двобічної критичної області

або , ураховуючи ту обставину, що критичні точки і симетрич­но розташовані відносно нуля.

 

57) Критерій узгодженості Пірсона. Критерій узгодженості Пірсона є випадковою величиною, що має розподіл , який визначається за формулою 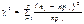і має k = q – m – 1 ступенів свободи, де q — число часткових інтервалів інтервального статистичного розподілу вибірки; m — число параметрів, якими визначається закон розподілу ймовірностей генеральної сукупності згідно з нульовою гіпотезою. Так, наприклад, для закону Пуассона, який характеризується одним параметром l, m = 1, для нормального закону m = 2, оскільки цей закон визначається двома параметрами i s. Якщо (усі емпіричні частоти збігаються з теоретичними), то , у противному разі . Визначивши при заданому рівні значущості a і числу ступенів свободи критичну точку , за таблицею (додаток 8) будується правобічна критична область. Якщо виявиться, що спостережуване значення критерію , то Н ₀ про закон розподілу ознаки генеральної сукупності відхиляється. У противному разі Н ₀ приймається.

58) Дисперсійний аналіз був створений спочатку для статистичної обробки агрономічних дослідів. В наш час його також використовують як в економічних експериментах, так і технічних, соціальних.

Сутність цього аналізу полягає в тому, що загальну дисперсію досліджуваної ознаки розділяють на окремі компоненти, які обумовлені впливом певних конкретних чинників. Істотність їх впливу на цю ознаку здійснюється методом дисперсійного аналізу.

Відповідно до дисперсійного аналізу будь-який його результат можна подати у вигляді суми певної кількості компонент. Так, наприклад, якщо досліджується вплив певного чинника на результат експерименту, то модель, що описує структуру останнього, можна подати так:

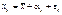,на j -му рівні фактора. Під рівнем фактора розуміють певну його міру. Наприклад, якщо фактором є добрива, які вносяться в ґрунт з метою збільшення врожайності сільськогосподарської культури, то рівнем фактора в цьому разі є кількість добрива, що вноситься в ґрунт; 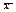— загальна середня величина ознаки Х; — ефект впливу фактора на значення ознаки Х на j -му рівні; — випадкова компонента, що впливає на значення ознаки Х в i -му експерименті на j -му рівні.

При цьому і як випадковi величини мають закон розподілу ймовірностей і між собою незалежні ().

У разі проведення дисперсійного аналізу досліджуваний масив даних, одержаних під час експерименту, поділяють на певні групи, які різняться дією на результати експерименту певних рівнів факторів.

Вважається, що досліджувана ознака має нормальний закон розподілу, а дисперсії в кожній окремій групі здобутих значень ознаки однакові. Ці припущення необхідно перевірити.

 

59) Однофакторний аналіз. Нехай потрібно дослідити вплив на ознаку Х певного одного фактора. Результати експерименту ділять на певне число груп, які відрізняються між собою ступенем дії фактора.

Для зручності в проведенні необхідних обчислень результати експерименту зводять в спеціальну таблицю:

Ступінь впливу фактора (групи)	Спостережуване значення ознаки Х	Групові середні	Загальна середня
			,
….	…	…
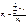
р

 

 

Таблиця результатів спостережень

Ступінь впливу фактора (групи)	Спостережуване значення ознаки Х	Групові середні	Загальна середня
			,
….	…	…
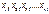
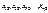
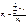
р