 - элементінің
- элементінің  миноры: осы анық. aij эль. бар i жолы j бағаны элем. сызыл.кейініг реті 1-ге тең.анықтау.
миноры: осы анық. aij эль. бар i жолы j бағаны элем. сызыл.кейініг реті 1-ге тең.анықтау.
 элементінің
элементінің 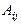 алгебралық толықтауышы төменгі теңдікпен анықталады Aij=(-1)i+jMij
алгебралық толықтауышы төменгі теңдікпен анықталады Aij=(-1)i+jMij
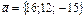 векторының модулін табыңыз 25
векторының модулін табыңыз 25
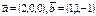 векторлары берілген.
векторлары берілген.  векторының ұзындығын есептеңіз 62
векторының ұзындығын есептеңіз 62
 және
және  векторлары
векторлары  мен
мен 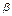 -ның қандай мәндерінде коллинеар болады? α=-1, β=4
-ның қандай мәндерінде коллинеар болады? α=-1, β=4
 векторының бағыттаушы косинустарын табыңыз cosα=12\25, cosβ=-3\5, cosλ=-16\25
векторының бағыттаушы косинустарын табыңыз cosα=12\25, cosβ=-3\5, cosλ=-16\25
 векторының базистік векторларымен жасайтын бұрыштарының косинустарын табыңдар cosα=1\3, cosβ=-2,3, cosλ=2\3
векторының базистік векторларымен жасайтын бұрыштарының косинустарын табыңдар cosα=1\3, cosβ=-2,3, cosλ=2\3
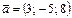 және
және  векторлары берілген. Осы векторлардың қосындысының модулін табыңдар 6
векторлары берілген. Осы векторлардың қосындысының модулін табыңдар 6
 және
және  векторларының арасындағы бұрышы
векторларының арасындағы бұрышы  -ге, ал олардың ұзындығы
-ге, ал олардың ұзындығы  ,
,  тең. Осы векторлардың скаляр көбейтіндісі тең:
тең. Осы векторлардың скаляр көбейтіндісі тең: 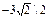
 векторының бірінші координатасы 6-ға, ал
векторының бірінші координатасы 6-ға, ал  -ке тең. Осы вектордың екінші координатасын табыңдар a1=(6;4), a2=(6;-4)
-ке тең. Осы вектордың екінші координатасын табыңдар a1=(6;4), a2=(6;-4)
 ;
;  ;
;  берілген.
берілген.  неге тең? -28
неге тең? -28
 ,
,  векторларының скаляр көбейтіндісін табыңыз 3
векторларының скаляр көбейтіндісін табыңыз 3
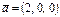 және
және  векторларынан құрылған бұрыштың косинусын табыңыз 0
векторларынан құрылған бұрыштың косинусын табыңыз 0
 ,
, 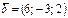 векторлары берілген. Осы векторлардың
векторлары берілген. Осы векторлардың  скаляр көбейтіндісін табыңыз 22
скаляр көбейтіндісін табыңыз 22
 және
және  векторлары
векторлары 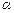 -нің қандай мәнінде өзара перпендикуляр болатынын анықтаңыз 6
-нің қандай мәнінде өзара перпендикуляр болатынын анықтаңыз 6
 және
және 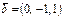 векторларына салынған параллелограмның ауданын табу керек. 3
векторларына салынған параллелограмның ауданын табу керек. 3
 және
және  векторлары берілген. Осы векторлардың арасындағы бұрыштың косинусын табыңыз 4\9
векторлары берілген. Осы векторлардың арасындағы бұрыштың косинусын табыңыз 4\9
 ,
, 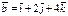 және
және  үш вектор берілген,
үш вектор берілген,  - табу керек 98
- табу керек 98
 және
және  векторларына салынған параллелограмның диагоналдарының арасындағы бұрышты табыңыз 900
векторларына салынған параллелограмның диагоналдарының арасындағы бұрышты табыңыз 900
 ,
,  , берілген.
, берілген.  -ны табыңыз 10
-ны табыңыз 10
 және
және  векторлары берілген. пр
векторлары берілген. пр  табыңыз 4√2\3
табыңыз 4√2\3
 және
және  векторларының векторлық көбейтіндісін табыңыз -i+j+k
векторларының векторлық көбейтіндісін табыңыз -i+j+k
 және
және  векторлары арасындағы бұрыштың синусын табыңыз 5√17\21
векторлары арасындағы бұрыштың синусын табыңыз 5√17\21
 және
және  векторларына салынған параллелограмның ауданын табыңыз 3
векторларына салынған параллелограмның ауданын табыңыз 3
 векторының модулін есептеу керек √10
векторының модулін есептеу керек √10
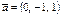 және
және  векторларына салынған параллелограмның ауданын есептеңіз √6
векторларына салынған параллелограмның ауданын есептеңіз √6
 ,
,  ,
,  векторларының аралас көбейтіндісін табыңыз 0
векторларының аралас көбейтіндісін табыңыз 0
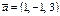 ,
,  ,
,  үш вектор берілген
үш вектор берілген 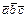 көбейтіндісін табыңыз. -7
көбейтіндісін табыңыз. -7
 және
және  векторлары коллинеар болады, егер x\x,=y\y,=z\z,
векторлары коллинеар болады, егер x\x,=y\y,=z\z,
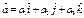 және
және  векторларының векторлық көбейтіндісі
векторларының векторлық көбейтіндісі  тең
тең 
 және
және 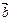 векторларының скаляр көбейтіндісі деп мына санды айтады |a||b|cos(a,b)
векторларының скаляр көбейтіндісі деп мына санды айтады |a||b|cos(a,b)
 векторының модулі тең |a|=√x2+y2+z2
векторының модулі тең |a|=√x2+y2+z2
 және
және 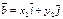 векторларының скаляр көбейтіндісі тең x1x2+y1y2
векторларының скаляр көбейтіндісі тең x1x2+y1y2
 және
және  векторларының скаляр көбейтіндісі тең x1x2+y1y2+z1z2
векторларының скаляр көбейтіндісі тең x1x2+y1y2+z1z2
 және
және 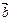 векторлары ортогонал болады, егер ab=0
векторлары ортогонал болады, егер ab=0
 ,
,  ,
,  . векторларының аралас көбейтіндісі
. векторларының аралас көбейтіндісі 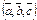 тең
тең 
 және
және 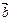 векторларының векторлық көбейтіндісі үшін мына қасиет орындалады ab=-(ba)
векторларының векторлық көбейтіндісі үшін мына қасиет орындалады ab=-(ba)
 векторларының компланар болуы үшін қажетті және жеткілікті шартын көрсет abc=0
векторларының компланар болуы үшін қажетті және жеткілікті шартын көрсет abc=0
 векторларының аралас көбейтіндісі үшін мына қасиет орындалады abc=-bac
векторларының аралас көбейтіндісі үшін мына қасиет орындалады abc=-bac
 және
және 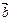 векторларының векторлық көбейтіндісі үшін мына қасиет орындалады a(b+c)=ab+ac
векторларының векторлық көбейтіндісі үшін мына қасиет орындалады a(b+c)=ab+ac
 және
және  векторлары
векторлары  -нің қандай мәнінде ортогонал болады -8
-нің қандай мәнінде ортогонал болады -8
 және
және 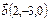 векторларының скаляр көбейтіндісін табыңыз 0
векторларының скаляр көбейтіндісін табыңыз 0
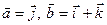 векторларының векторлық көбейтіндісін табыңыз i-k
векторларының векторлық көбейтіндісін табыңыз i-k
 және
және  коллинеар векторлардың векторлық көбейтіндісін табыңыз 0
коллинеар векторлардың векторлық көбейтіндісін табыңыз 0
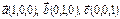 векторына салынған параллелепипедтің көлемін табыңыз (1)
векторына салынған параллелепипедтің көлемін табыңыз (1)
 және
және 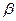 -ның қандай мәндерінде
-ның қандай мәндерінде  және
және 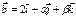 коллинеарлы α=4,β=-6
коллинеарлы α=4,β=-6
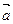 векторының
векторының  векторына проекциясы неге тең? a*b\|b|
векторына проекциясы неге тең? a*b\|b|
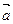 ,
,  және
және  векторларының компланар болуының қажетті және жеткілікті шартын көрсет abc=0
векторларының компланар болуының қажетті және жеткілікті шартын көрсет abc=0
 және
және  векторларының скаляр көбейтіндісін табыңыз 0
векторларының скаляр көбейтіндісін табыңыз 0
 және
және  векторлары
векторлары  -нің қандай мәнінде өзара перпендикуляр болды? 4
-нің қандай мәнінде өзара перпендикуляр болды? 4
 және
және  векторлары
векторлары  -нің қандай мәнінде ортогонал болды? 1
-нің қандай мәнінде ортогонал болды? 1
 векторларының аралас көбейтіндісін табыңыз 4
векторларының аралас көбейтіндісін табыңыз 4
 жарты өсімен және
жарты өсімен және  фокусымен берілген эллипстің теңдеуін жазыңыз x2\64+y2\28=1
фокусымен берілген эллипстің теңдеуін жазыңыз x2\64+y2\28=1
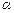 шексіз аз болғанда эквиваленттік шаманы көрсетіңіз:
шексіз аз болғанда эквиваленттік шаманы көрсетіңіз:
 кесіндісіндегі
кесіндісіндегі  функциясының анықталған интегралы
функциясының анықталған интегралы 
|a|=3, |b|=4 (a,b)=π\6 болса...паралеограмнын ауд 6
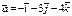 ,
, 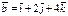 және
және 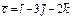 үш вектор берілген,
үш вектор берілген,  - табу керек 98
- табу керек 98
 және
және  векторлары берілген. Егер
векторлары берілген. Егер  шарты орындалса, онда
шарты орындалса, онда 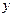 координатасын табыңыз -4
координатасын табыңыз -4
 векторының бірлік векторын табыңыз
векторының бірлік векторын табыңыз
(3\13;4\13;-12\13)
 векторының бірлік векторын табыңыз a=-6\7i+2\7j-3\7k
векторының бірлік векторын табыңыз a=-6\7i+2\7j-3\7k






