Аффинным пространство называется мно-во точек и векторов, элементы которого находятся в отношениях, определённых аксиомами откладывания вектора и умножения вектора на число.
Линейно независимая система векторов называется базисом аффинного пространства, если любой вектор этого пространства может быть представлен виде линейной комбинации этих векторов.
Размерность определяется кол-вом векторов, которые могут составлять базис.
прямая, плоскость и пространство.
Доказать теорему о существовании и единственности разложения вектора по произвольному базису. Координаты векторов.
Т: Каждый вектор аффинного пространства может быть представлен в виде линейной комбинации базиса и при том только единственным образом.
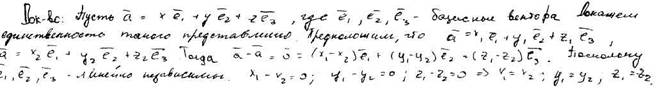
О: Упорядоченная тройка чисел x,y,z, определяющая разложение вектора по базису называется координатами вектора в этом базисе.
Аффинная система координат. Радиус-вектор. Координаты точки. Доказать теорему о координатах векторов.
Совокупность произвольной точки (начала координат) и векторов, е1, е2 и е3, образующих базис называют аффинной системой координат.
Радиус-вектор точки, это вектор, отложенный из начала координат к этой точке.
Упорядоченная тройка чисел (x, y, z), являющаяся координатами радауса-вектора точки А, называется координатами точки а в этом базисе.
Т: Координаты вектора в произвольном базисе равны разности координат точки конци и начала вектора в этом базисе.

Доказать теорему о координатах суммы векторов.
Т: Координаты суммы двух векторов равны сумм координат этих векторов.
Доказывается сложением векторов, представленных в виде линейной комбинации базисных.
Аффинное пространство. Доказать теорему о координатах вектора, умноженного на число.
Аффинным пространство называется мно-во точек и векторов, элементы которого находятся в отношениях, определённых аксиомами откладывания вектора и умножения вектора на число.
Т: Координаты вектора, умноженного на число, равны координатам вектора, умноженным на это число.
Вектор, представляется в виде линейной комбинации базисных векторов, а потом правая и левая часть умножаются на некое число и раскрываются скобки.
Доказать теорему о разложении радиус-вектора точки, делящей отрезок в данном отношении.
Доказывается через сложение векторов по правило треугольника.
Определение прямой. Вывести векторное уравнение прямой в аффинной системе.
Множество всех точек М, для которых векторы АМ и АВ коллинеарны, называется прямой (АВ).







