Задача1. Предприятие А выпускает комплектующие изделия для предприятия В. Требуется определить оптимальную частоту контроля предприятием В за качеством комплектующих изделий, выпускаемых А, чтобы затраты на контроль и затраты, зависящие от качества выпускаемой продукции, были минимальны. При уменьшении частоты контроля увеличивается поток брака со стороны А и прибыли В уменьшается. При увеличении частоты контроля качество продукции предприятия В увеличивается, но при этом стоимость контроля увеличивается.
Пусть потери и прибыль предприятия В состоят из:
- 50 тыс. руб. потерь от поставки предприятием А бракованных комплектующих;
- 5 тыс. руб. затраты на контроль комплектующих;
- 10 тыс. руб. премия предприятию А за поставку годных комплектующих;
- 140 тыс. руб. штрафа, налагаемого на предприятие А в случае обнаружения брака.
Используя теорию игр, определить оптимальную стратегию предприятия В.
Составим игровую задачу.
Предположим, что со стороны А могут быть следующие стратегии i:
х1- предприятие поставляет полностью брак;
х2- предприятие поставляет годные комплектующие;
х3- предприятие поставляет 50% брака.
Со стороны В возможны следующие стратегии j:
y1- предприятие полностью контролирует комплектующие;
y2- контролирует 75%;
y3- контролирует 50%;
y4- контролирует 25%.
Для составления матрицы игры введем следующие понятия:
оценка степени контроля Рy=(1; 0,75; 0,5; 0,25);
оценка степени брака Рх=(1; 0; 0,5);
оценка степени обнаружения брака Рб= Рх ∙ Рy;
оценка степени пропуска брака Р=(1- Рy) Рх .
Потери сторон рассчитаем по формуле:
LA=LB=140Pб -50P-5Py-10(1-Pб).
В этом случае таблица игры примет вид:
| А В | х1 | х2 | х3 |
| y1 | -15 | ||
| y2 | -14 | ||
| y3 | -12 | -12 | |
| y4 | -10 | -10 | -10 |
Чтобы исключить отрицательные потери, каждое из значений увеличиваем на 15. В результате получим матрицу.
| А В | х1 | х2 | х3 | max(a) min |
| y1 | ||||
| y2 | ||||
| y3 | ||||
| y4 | 
| 5* | ||
| max() min | 5* |
Определим цены игры a и b.
, 
, следовательно, со стороны А оптимальная стратегия х2 (0% брака), со стороны В- y4 (25% контроль). При этом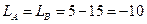 
., т.е. выигрыш стратегии А и проигрыш стратегии В равняется 10 тыс. рублей.
Задача 2. АСУ может быть оснащена ЭВМ трёх типов. На обработку в АСУ будут приниматься задачи трёх видов. Решение задачи требует определенного времени, зависящего от характеристик ЭВМ, сложности и объема задач. Расходы на содержание АСУ оплачивает поставщик задач (заказчик).
Сторона А (организатор АСУ), располагает 3-мя стратегиями по выбору машин i (x1, x2, x3) и стремится увеличить приток средств от заказчика за счет ускорения обработки заказов и даже применяет дорогостоящие ЭВМ там, где можно было бы обойтись простыми машинами.
Сторона В (заказчик) старается разумно расходовать свои средства, отказываясь от чрезмерных требований по срокам, корректно формулирует задачи, выбирает те из них, которые представляют первоочередной интерес. Исходя из этого, заказчик обращается к АСУ для решения трёх видов задач (y1, y2, y3,).
В соответствии с калькуляцией стоимость выполнения работ qij в рублях, следующая.На первой ЭВМ первой задачи q11 = 250, второй задачи q12 = 300, и третьей задачи q 13 = 350.
Стоимость работы на второй ЭВМ при выполнении соответствующих задач q21 =300, q22 =400, q23 =600.
Стоимость работы на третьей ЭВМ: q31 =400, q32 =500, q33 =600. Рассматривая задачу как игровую, необходимо определить какой из трёх машин необходимо комплектовать АСУ.
