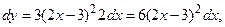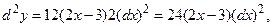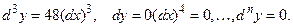ОДНОЙ ПЕРЕМЕННОЙ
Дифференцирование функций
Производной функции y = f(x) в точке х называется предел отношения приращения функции к приращению аргумента, когда при-ращение аргумента стремится к нулю:
где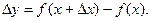 
Производная обозначается у', y' (x), y'x.
Правила дифференцирования функций. Пусть С – постоянная, а u(x) и v(x) – дифференцируемые функции. Тогда C' = 0,
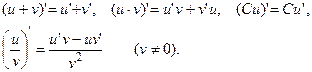
Производная сложной функции y = f (u (x)). Если функция u = u (x) дифференцируема в точке х, а функция y = f(u) дифференцируемая в соответствующей точке u = u (x), то сложная функция y = f (u (x)) дифференцируема в точке х и ее производная равна
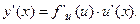
Таблица производных.
1. 
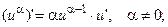
2. 
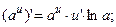
3. 
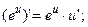
4. 
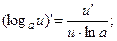
5. 
6. 
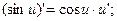
7. 
8. (
9. 
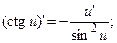
10. 
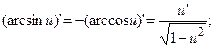
11. 
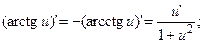
12. 
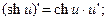
13. 
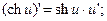
14. 
Функция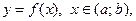 
неявно задана уравнением 
если для всех 
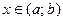выполняется равенство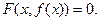 
Для вычисления производной функции, заданной неявно, следует тождество 
продифференцировать по х (рассматривая левую часть как сложную функцию от х), а затем полученное уравнение решить относительно f'(x).
Пример 6.1. Найти производную показательно-степенной функции
.
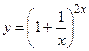Решение. Логарифмируя, а затем дифференцируя левую и правую части, получим
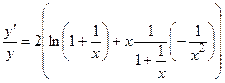
Умножая обе части равенства на у, имеем:
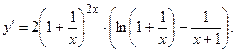
Пример 6.2. Найти производную функции 
, заданной неявно уравнением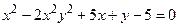 
.
Решение. Дифференцируя по х тождество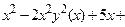 
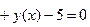, получим 
. Выражая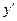 
из этого равенства, находим:
.
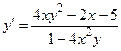Дифференциал 
функции равен произведению ее про-изводной на приращение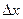 
независимой переменной: 
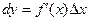или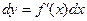 
.
При достаточно малых 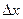имеет место приближенная формула 
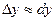, т.е. 
или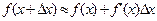 
.
Пример 6.3. Найти приближенное значение объема шара, радиус которого равен 1,02 м.
Решение. Воспользуемся формулой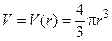 
. Тогда 
. Полагая 
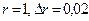, получим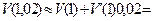 
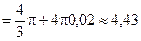м3.
Производные и дифференциалы высших порядков.
Дифференцирование функций, заданных параметрически
Производной второго порядка функции называется производная от ее производной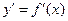 
, т.е. 
. Аналогично определяются производные более высоких порядков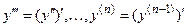 
.
Дифференциалы высших порядков функции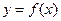 
(x – независимая переменная) вычисляются по формулам
.
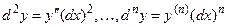Если функция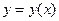 
задана параметрически соотношениями 
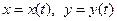, причем 
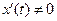, то ее первая 
и вторая 
производные находятся по формулам:
.
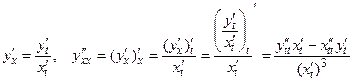Пример 6.4. Найти выражение для производной n- го порядка функции 
.
Решение.
.
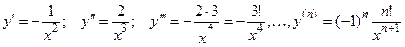Пример 6.5. Найти производную 2-го порядка от функции 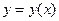, заданной неявно уравнением 
.
Решение. По правилу дифференцирования функции, заданной неявно, получаем:
.
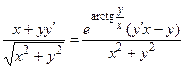Отсюда, используя равенство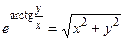 
, имеем:
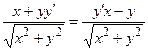или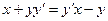 
.
Следовательно,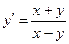 
.
Дифференцируя последнее равенство и используя найденное для 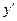выражение, получим:
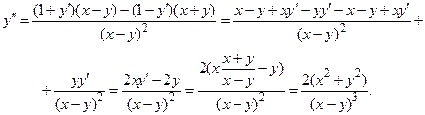
Пример 6.6. Найти производную 2-го порядка функции, заданной параметрически: 
Решение.
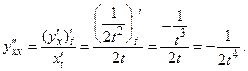
Пример 6.7. Найти дифференциалы 1-го, 2-го, …, n -го порядков функции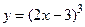 
.
Решение.
