При выполнении контрольных работ необходимо строго придер-живаться указанных ниже правил. Работы, выполненные без соблю-дения этих правил, не зачитываются и возвращаются студенту для переработки.
1. Каждая контрольная работа должна быть выполнена в отдельной тетради в клетку чернилами любого цвета, кроме красного. Необходимо оставлять поля шириной 4–5 см для замечаний рецензента.
2. В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), название дисциплины, номер контрольной работы, номер варианта; здесь же следует указать название учебного заведения, дату отсылки работы в университет и адрес студента. В конце работы следует поставить дату ее выполнения и подпись студента.
3. В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту. Контрольные работы, содержащие не все задачи, а также задачи не своего варианта, не зачи-тываются.
4. Решения задач надо располагать в порядке возрастания их номеров, указанных в заданиях, сохраняя номера задач.
5. Перед решением каждой задачи надо полностью выписать ее условие. В том случае, если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, сле-дует, переписывая условие задачи, заменить общие данные конкрет-ными, взятыми из соответствующего номера.
Условие задачи должно быть написано так:
Найти работу, произведенную силой 
, если ее точка приложения перемещается из точки 
в точку 
.
Р е ш е н и е
______________________________________________
Ответ: А = 10.
6. Решения задач следует излагать подробно и аккуратно, кратко и лаконично объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи. Каждую задачу желательно начинать с новой страницы.
7. После получения прорецензированной работы, как не зачтенной, так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента.
Если рецензент предлагает внести в решение задач те или иные исправления и дополнения, то в случае не зачтенной контрольной работы ее следует представить на повторную рецензию в короткий срок.
При повторном представлении работы должна обязательно нахо-диться прорецензированная работа и рецензия на нее. Поэтому при выполнении контрольной работы рекомендуется оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента.
ПРОГРАММА
Элементы линейной алгебры
И аналитической геометрии
1. Системы координат на прямой, плоскости и в пространстве. Про-странства 
и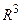 
. Векторы. Линейные операции над векторами. Проекция вектора на ось. Направляющие косинусы и длина вектора. Понятие о векторных диаграммах в науке и технике (диаграммы сил, моментов сил, электрических токов, напряжений и др.). Координаты центра масс.
2. Скалярное произведение векторов и его свойства. Длина вектора и угол между двумя векторами в координатной форме. Условие ортогональности двух векторов. Механический смысл скалярного произведения.
3. Определители второго и третьего порядков, их свойства. Алгебраические дополнения и миноры. Определители n -го порядка. Вы-числение определителя разложением по строке (столбцу).
4. Векторное произведение двух векторов, его свойства. Условие коллинеарности двух векторов. Геометрический смысл определителя второго порядка. Простейшие приложения векторного произведения в науке и технике: моменты сил, сила, действующая на проводник с током в магнитном поле, скорость точки вращающегося тела, направление распространения электромагнитных волн.
5. Смешанное произведение векторов. Геометрический смысл оп-ределителя третьего порядка.
6. Уравнения линий на плоскости. Различные формы уравнения прямой на плоскости. Угол между прямыми. Расстояние от точки до прямой.
7. Кривые второго порядка: окружность, эллипс, гипербола, пара-бола, их геометрические свойства и уравнения. Технические прило-жения геометрических свойств кривых (использование фокальных свойств, математические модели формообразования биологических, технических и других объектов).
8. Уравнения плоскости и прямой в пространстве. Угол между плос-костями. Угол между прямыми. Угол между прямой и плоскостью.
9. Уравнение поверхности в пространстве. Цилиндрические поверхности. Сфера. Эллипсоид. Гиперболоиды. Параболоиды. Геомет-рические свойства этих поверхностей, исследование их формы методом сечений. Технические приложения геометрических свойств поверхностей (использование фокальных свойств, модели строитель-ных конструкций, физические модели элементов и т.п.).
10. Полярные координаты на плоскости. Спираль Архимеда.
11. Цилиндрические и сферические координаты в пространстве. Различные способы задания линий и поверхностей в пространстве.
12. Матрицы, действия с ними. Понятие обратной матрицы.
13. Системы двух и трех линейных уравнений. Матричная запись системы линейных уравнений. Правило Крамера. Система m линейных уравнений с n неизвестными. Метод Гаусса. Нахождение обратной матрицы методом Гаусса.
14. Пространство 
. Линейные операции над векторами. Различ-ные нормы в . Скалярное произведение в .
15. Линейные и квадратичные формы в . Условие знакоопределенности квадратичной формы.
16. Понятие линейного (векторного) пространства. Вектор как эле-мент линейного пространства. Примеры. Линейные операторы. При-меры линейных операторов. Применение линейных операторов для моделирования различных процессов.
Введение в математический анализ
17. Элементы математической логики: необходимое и достаточное условия. Прямая и обратная теоремы. Символы математической логики, их использование. Бином Ньютона. Формулы сокращенного умножения.
18. Множество действительных чисел. Функция. Область ее определения. Способы задания. Основные элементарные функции, их свойства и графики.
19. Числовые последовательности, их роль в вычислительных процессах. Предел числовой последовательности. Стабилизация десятичных знаков у членов последовательности, имеющей предел. Существование предела монотонной ограниченной последовательности.
20. Сложные и обратные функции, их графики. Класс элементар-ных функций.
21. Предел функции в точке. Предел функции в бесконечности. Пределы монотонных функций.
22. Непрерывность функций в точке. Непрерывность основных эле-ментарных функций.
23. Бесконечно малые в точке функции, их свойства. Сравнение бесконечно малых. Символы о и О.
24. Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего и наименьшего значений, существование промежуточных значений.
