Пусть задана система n линейных уравнений с n неизвестными вида
(4.1)
или, в матричной форме
А Х = В,
где
Рассмотрим некоторые методы решения системы (4.1).
Формулы Крамера. Если система (4.1) невырождена, то она имеет единственное решение, определяемое формулами Крамера:
где 
– определитель, получаемый из определителя 
заменой его i- го столбца на столбец В свободных членов.
Матричный метод.
Решение невырожденной системы (4.1) можно найти по формуле 
.
Метод последовательного исключения неизвестных (метод Гаусса).
С помощью элементарных преобразований над строками система m линейных уравнений с n неизвестными может быть приведена к виду
, (4.2)
где 
Система (4.2) эквивалентна исходной системе. Если хотя бы одно из чисел 
отлично от нуля, то система (4.2), а следовательно, и исходная система несовместны. Если же 
то система совместна и из уравнений (4.2) выражают последовательно неизвестные 
через 
.
Пример 4.2. Методом Гаусса решить систему
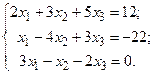
Решение. Расширенная матрица системы имеет вид
Производя элементарные преобразования над строками расширенной матрицы, получаем
где цифрами 
обозначены следующие операции:
– первую и вторую строки поменяли местами; 
– ко второй строке прибавили первую, умноженную на (–2); к третьей прибавили первую, умноженную на (–3); 
– к третьей строке прибавили вторую, умноженную на (–1).
Этой матрице соответствует система
Отсюда последовательно находим
Ответ: 
Пример 4.3. Решить систему уравнений
используя формулы Крамера.
Решение. Так как определитель данной системы
то матрица А невырождена и система имеет единственное решение.
Находим определители 
По формулам Крамера находим решение системы:
4.3. Скалярное произведение векторов в R 3
Скалярным произведением векторов 
и 
называется число, обозначаемое 
или 
и равное 
где 
– угол между и .
Свойства скалярного произведения:
1. 
2. 
3. 
4. 
Свойство 4 выражает условие ортогональности векторов.
Если векторы 
и 
представлены своими координатами в ортонормированном базисе 
, то скалярное про-изведение равно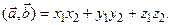 
Из этой формулы и определения скалярного произведения следует:
Учитывая, что 
где 
– проекция вектора на вектор , а 
скалярное произведение векторов 
можно записать в виде
Пример 4.4. Даны векторы 
Найти 
.
Решение.
Поскольку 
а векторы заданы координатами в ортонормированном базисе, то
Поэтому
Механический смысл скалярного произведения: работа А, про-изводимая силой 
точка приложения которой перемещается из точки 
в точку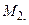 
вычисляется по формуле 
