Функция 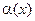 называется бесконечно малой при
называется бесконечно малой при 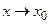 , если
, если  . Пусть
. Пусть 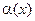 и
и  – бесконечно малые при
– бесконечно малые при 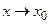 и существует предел их отношения
и существует предел их отношения 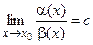 . Если
. Если 
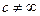 , то
, то 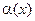 и
и  называются бесконечно малыми одного
называются бесконечно малыми одного
порядка малости. Обозначение 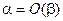 при
при 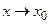 . Если с = 1, то
. Если с = 1, то 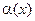 и
и  называются эквивалентными бесконечно малыми (обозначение:
называются эквивалентными бесконечно малыми (обозначение: 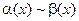 при
при 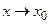 ). Если с = 0, то
). Если с = 0, то 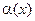 называется бесконечно малой высшего порядка, чем
называется бесконечно малой высшего порядка, чем  (обозначение
(обозначение 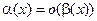 при
при 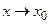 ).
).
При нахождении предела отношения двух бесконечно малых функций каждую из них можно заменить эквивалентной ей бесконечно малой, т.е. если 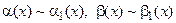 при
при 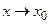 , то
, то
 .
.
Пример 5.1. Найти 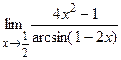 .
.
Решение. При  функции
функции 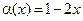 и
и 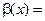
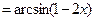 являются эквивалентными бесконечно малыми. Поэтому
являются эквивалентными бесконечно малыми. Поэтому
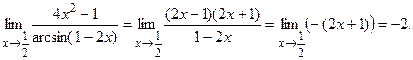
Функция 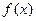 называется бесконечно большой при
называется бесконечно большой при 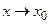 , если для любого положительного числа М существует такое число
, если для любого положительного числа М существует такое число  , что при всех х, удовлетворяющих условию
, что при всех х, удовлетворяющих условию 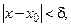
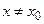 , выполняется неравенство
, выполняется неравенство  .
.
Обозначение
 .
.
Функция 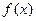 называется непрерывной в точке
называется непрерывной в точке  , если:
, если:
1) функция 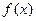 определена в точке
определена в точке  и ее окрестности;
и ее окрестности;
2) существует конечный предел функции 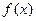 в точке
в точке  ;
;
3) этот предел равен значению функции в точке  , т.е.
, т.е.

На практике часто используют другое определение непрерывности функции в точке, равносильное данному.
Функция 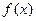 называется непрерывной в точке
называется непрерывной в точке  , если выпол-няются условия:
, если выпол-няются условия:
1) функция 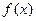 определена в точке
определена в точке  и ее окрестности;
и ее окрестности;
2) существуют конечные односторонние пределы
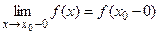 и
и 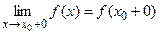 ;
;
3) эти пределы равны между собой и равны значению функции в точке  .
.
Укажем основные свойства непрерывных функций.
1. Простейшие элементарные функции (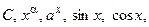
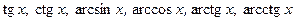 ) непрерывны во всех точках, где они определены.
) непрерывны во всех точках, где они определены.
2. Если функции 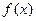 и
и  непрерывны в точке
непрерывны в точке  , то и функции
, то и функции  непрерывны в точке
непрерывны в точке  .
.
3. Если 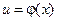 непрерывна в точке
непрерывна в точке  , а
, а  непрерывна в точке
непрерывна в точке 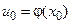 , то сложная функция
, то сложная функция 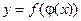 непрерывна в точке
непрерывна в точке  .
.
4. Если функция  непрерывна на отрезке
непрерывна на отрезке  и возрастает (или убывает) на этом отрезке, то обратная функция
и возрастает (или убывает) на этом отрезке, то обратная функция  на соответствующем отрезке оси
на соответствующем отрезке оси 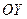 существует и является также непрерывной возрастающей (убывающей) функцией.
существует и является также непрерывной возрастающей (убывающей) функцией.
Точка  , в которой не выполняется хотя бы одно из трех условий непрерывности функции, называется точкой разрыва функции.
, в которой не выполняется хотя бы одно из трех условий непрерывности функции, называется точкой разрыва функции.
Если в точке  существуют конечные односторонние пределы
существуют конечные односторонние пределы 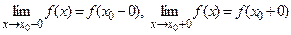 , такие что
, такие что 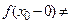
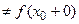 , то
, то  называется точкой разрыва первого рода. Если хотя бы один из пределов
называется точкой разрыва первого рода. Если хотя бы один из пределов  не существует или равен бесконечности, то точка
не существует или равен бесконечности, то точка  называется точкой разрыва второго рода. Если
называется точкой разрыва второго рода. Если 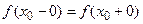 , но функция в точке
, но функция в точке  не определена или если
не определена или если 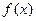 в точке
в точке  определена, но
определена, но 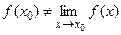 , то
, то  называется точкой устранимого разрыва.
называется точкой устранимого разрыва.
Пример 5.2. Найти точки разрыва функции 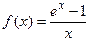 и определить их вид.
и определить их вид.
Решение. Так как функции  и
и 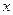 непрерывны, то непрерывным будет и их отношение
непрерывны, то непрерывным будет и их отношение 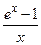 во всех точках, кроме точки
во всех точках, кроме точки 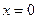 . При
. При 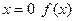 не определена, следовательно, разрывна. Так как
не определена, следовательно, разрывна. Так как  (см. п. 5.1 пример 12), то
(см. п. 5.1 пример 12), то 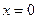 – точка устранимого разрыва. Если положить
– точка устранимого разрыва. Если положить 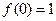 , то функция
, то функция
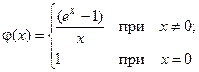
будет непрерывной при всех  .
.
Пример5.3. Установить вид точек разрыва функции
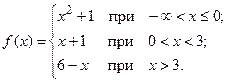
Решение. Область определения функции 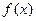 – вся числовая ось
– вся числовая ось  . Разрывы возможны только в точках
. Разрывы возможны только в точках 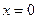 и
и  , в которых изменяется аналитическое задание функции. Найдем односторонние пределы в точке
, в которых изменяется аналитическое задание функции. Найдем односторонние пределы в точке 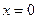 и значение функции в этой точке:
и значение функции в этой точке:

Следовательно, в точке 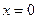 функция непрерывна.
функция непрерывна.
Рассмотрим точку  :
:
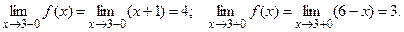
Так как эти пределы конечны но не равны между собой, то х = 3 – точка разрыва первого рода. График функции f(x) изображен на рис. 5.1.
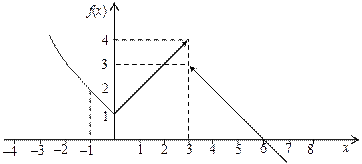
Рис. 5.1
Пример 5.4. Установить вид точек разрыва функции

Решение. Данная функция непрерывна всюду, кроме точки
х = –1, в которой f (x) не определена.
Поскольку
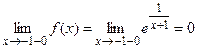 (т.к.
(т.к. 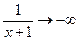 при
при 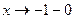 ),
),
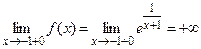 (т.к.
(т.к.  при
при 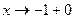 ),
),
т.е. правосторонний предел бесконечен, то х = –1 – точка разрыва второго рода.






