Ранее мы считали, что a priori известны:
1. условные совместные плотности распределения шума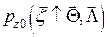 
и аддитивной смеси сигнала и шума 
,
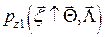2. вероятности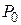 
отсутствия сигнала в наблюдаемой реализации сигнала 
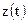и наличия в ней сигнала 
,
3. платежная матрица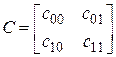 
с элементами 
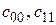- расходы на принятие правильные решения и 
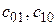- плата за ошибки первого и второго рода.
В общем случае неопределенными могут быть любые данные.
Если неизвестны только параметры совместных плотностей распределения, то говорят о параметрической априорной неопределенности.
Если же заранее неизвестны сами плотности распределения, то говорят о непараметрической неопределенности.
Неизвестные параметры, существенные для формулировки задачи, считаются полезными, остальные – мешающими. Так, в задаче обнаружения гармонического сигнала на фоне помех, полезным параметром является амплитуда колебания, а частота и фаза – это несущественные, мешающие параметры.
1. Первые попытки преодоления априорной неопределенности были сделаны еще в рамках классического байесовского подхода. Неизвестные параметры функций распределения помехи и смеси помехи и сигнала трактовались как случайные величины с известными распределениями. В этом случае приходится усреднять по этим неизвестным параметрам и отношение правдоподобия, и ошибки обнаружения, и средний риск, связанный с ошибками обнаружения.
2. Если нет априорных сведений о величинах потерь, то есть неизвестна платежная матрица, и неизвестны априорные вероятности наличия или отсутствия сигнала в исходной выборке, то поступают следующим образом:
- потери, связанные с принятием правильных решений, принимаются равными нулю (
),
- потери, связанные с принятием ошибочных решений, считаются одинаковыми,
- априорные вероятности наличия или отсутствия сигнала, принимаются одинаковыми (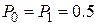
).
Но вид плотностей распределения должен быть известен с точностью до полезных параметров. Вариации мешающих параметров делают алгоритм неустойчивым. Эффективность применения алгоритма становится зависящей от значений мешающих параметров.
3. Одним из самых распространенных критериев в задачах обнаружения сигналов является критерий Неймана – Пирсона.
Сущность его заключается в том, что из всех возможных алгоритмов выбирают тот, при котором обеспечивается максимум вероятности правильного обнаружения сигнала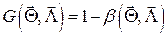 
при условии, что вероятность ложной тревоги 
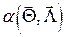не превысит некоторого заданного значения 
.
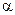В случае параметрической априорной неопределенности стараются выбрать такое правило принятия решения, которое, при заданном 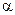, обеспечивало бы максимум мощности 
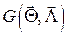при любых значениях параметров сигнала и шума. Такие алгоритмы называются равномерно наиболее мощными. Они, правда, существуют далеко не всегда.
4. Для получения приемлемого решения в предыдущих условиях часто приходится ограничиваться только такими алгоритмами, для которых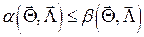 
. Такие алгоритмы называются несмещенными.
5. В непараметрическом случае, когда неизвестны даже априорные плотности распределения, а известно лишь, что они существенно отличаются от нормального распределения, обычно применяется следующий подход: ищут такие статистики, то есть такие функции выборочных значений принимаемого сигнала, которые бы в широких пределах не зависели от распределения значений шума. Так в примере мы использовали среднее арифметическое из имеющихся выборочных значений. Его распределение можно считать нормальным независимо от распределения выборки в широком классе симметричных распределений.
6. Синтез оптимальных непараметрических алгоритмов обнаружения связан с практически непреодолимыми математическими трудностями. Решить проблему удается лишь в асимптотических случаях, когда число отсчетов сигнала стремится к бесконечности. В этом случае отношение правдоподобия оказывается величиной, распределенной нормально и поэтому непараметрическая неопределенность переходит в параметрическую.
7. Промежуточное положение между параметрическими и непараметрическими алгоритмами обнаружения сигналов в условиях априорной неопределенности занимают робастные алгоритмы. Основная идея их применения связана с тем, что распределение выборочных данных хотя и неизвестно, но не может быть произвольным. О нем всегда имеется хотя бы некоторая информация. Это позволяет найти множество возможных распределений шума и построить алгоритм, минимизирующий максимальное ухудшение качества обнаружения сигнала на этом множестве распределений.
[1] Здесь под функцией векторов понимается просто функция многих переменных – компонент этих векторов. Эти компоненты для удобства просто собраны в отдельные группы, которые и рассматриваются как вектора.
