Постановка задачи обнаружения сигналов

Процедуры обнаружения и различения сигналов на фоне помех

Последняя книга по этому поводу:

В.А. Богданович и А.Г. Вострецов. Теория устойчивого обнаружения, различения и оценивания сигналов.- М. ФИЗМАТЛИТ, 2004.

Постановка задачи обнаружения сигналов

Процедуры обнаружения и различения сигналов применяются в тех случаях, когда:

- влияние помех настолько велико, что обычные методы преобразования сигналов не приводят к положительным результатам,

- априорной информации совершенно недостаточно для того, чтобы «узнать» сигнал на фоне шумов, отличить его от шума.

Для примера на рис. 1 представлены графики смеси сигнала и шума A(t)+z(t), самого сигнала z(t) и только шума A(t).

На глаз на верхнем графике невозможно обнаружить что-то, отличное от шума, особенно если у нас нет никакой априорной информации о форме сигнала и его параметрах – моменте возникновения, длительности, амплитуде и частоте. Такая ситуация типична для программы поиска сигналов внеземных цивилизаций.

Вы уже поняли, что априорная информация является одним из основных факторов, определяющих действенность процедур контроля, распознавания образов, диагностики идентификации систем.

При полном отсутствии априорной информации сбор и обработка данных бессмысленна – невозможно найти «то, не знаю, что». При наличии априори всей информации об объекте исследования применение каких-либо измерительных информационных технологий так же совершенно лишено смысла – мы и без того все знаем. При работе измерительных информационных систем любого назначения мы всегда сталкиваемся с недостаточностью априорной информации. Задача почти всегда заключается в том, чтобы получить как можно больше апостериорной информации, используя как можно лучше все имеющиеся априорные сведения.

В задачах обнаружения сигнала неизвестным является сам факт наличия сигнала. Априорной информацией здесь могут быть сведения о форме сигнала, о частотах его появления, вероятности существования и прочее.

В задачах различения сигналов неизвестен тип принимаемого в данный момент сигнала из заданного множества возможных типов сигналов. В качестве априорной информации здесь используются сведения о возможных видах сигналов и вероятности появления различных типов сигналов.

В задачах оценивания сигналов неизвестным является значение сигнала или вектор (совокупность) параметров сигнала. Априори хорошо бы иметь сведения о форме сигнала и распределении вероятностей его параметров.

Остальные компоненты сигнально - помеховой обстановки считаются, как правило, известными. Априори известно статистическое описание помех, значения неинформативных параметров сигнала, условия проведения эксперимента.

В простейших случаях задача обнаружения сигналов сводится к использованию специальных фильтров, повышающих отношение сигнал/шум:

где - мощность сигнала на промежутке Т его существования,

- мощность шума .

Рассмотрим вопросы применимости различных типов фильтров.

Частотная фильтрация.

Предположим, что передаваемый кодированный сигнал имеет форму отрезков синусоиды:

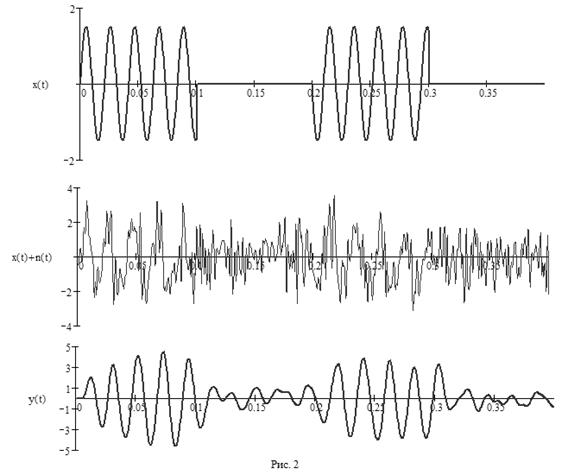
На рис. 2 сверху представлен отрезок сигнала x(t), а в середине – тот же сигнал, но в смеси с белым шумом n(t). Здесь нужно иметь большое воображение, чтобы заметить следы сигнала x(t) на фоне шума.

Для выделения сигнала естественно использовать полосовой фильтр с узкой полосой пропускания, средняя частота которого равна частоте сигнала .

На рис. 2 внизу представлен сигнал y(t) на выходе резонансного фильтра, настроенного на частоту сигнала x(t) при степени успокоения 0,2. Дифференциальное уравнение фильтра и порядок его решения в среде Math Cad представлено в листинге:

На графике (рис. 2) уже можно четко заметить полезный сигнал, несмотря на имеющие место искажения остатками шума.

 

Пусть n(t) – белый широкополосный шум с мощностью в полосе частот до . В этом случае мощность шума на выходе фильтра с полосой пропускания вокруг частоты составит:

.

Казалось бы, что, уменьшая полосу пропускания фильтра по отношению к полосе частот, занимаемых шумом, можно как угодно увеличивать отношение сигнал/шум и тем самым все более четко определять наличие сигнала на фоне шума.

Однако здесь следует иметь в виду следующее обстоятельство. Спектр синусоидального сигнала сосредоточен на его частоте только в том случае, когда эта синусоида задана на всем промежутке времени от до .

Отрезок синусоиды конечной протяженности имеет лепестковый спектр (рис. 3), главный максимум которого приходится на частоту сигнала . Полосовой фильтр обязательно поглощает часть энергии полезного сигнала вместе с энергией шума, что приводит к амплитудным и фазовым искажениям сигнала. Это хорошо видно на нижнем графике, на рис. 2.

Временная фильтрация

Будем по-прежнему считать, что принимаемый сигнал – это радиоимпульс:

Принимаемый сигнал является аддитивной смесью сигнала и шума:

.

Определим автокорреляционную функцию этой смеси:

Если сигнал и шум не коррелированны, то их взаимнокорреляционная функция равна нулю, и поэтому автокорреляционная функция аддитивной смеси сигнала и шума равна сумме их автокорреляционных функций:

Если x(t) – синусоидальный сигнал со случайной фазой, то его автокорреляционная функция является косинусоидой той же частоты:

Автокорреляционная функция шума обычно быстро убывает с ростом τ, а для белого шума имеет форму δ – функции при τ=0. Поэтому автокорреляционная функция синусоидального сигнала на фоне почти белого шума будет всегда выглядеть так, как это показано на рис. 4 слева. При отсутствии сигнала () автокорреляционная функция будет просто быстро затухать, как на рис. 4 справа. Отсчет значения автокорреляционной функции по истечении времени в первом случае даст значение , а во втором случае – нуль.

Это обстоятельство и положено в основу построения временных (корреляционных) фильтров. Схема построения фильтра представлена на рис. 5.

Фильтр состоит из линии задержки на время , схемы перемножения принимаемого сигнала и сигнала на выходе линии задержки и интегратора, обеспечивающего интегрирование результата перемножения по времени в пределах от 0 до , после чего интегратор обнуляется и вновь включается в момент ожидаемого прихода нового радиоимпульса. Название этого устройства фильтром является в большой степени условным, поскольку он осуществляет не преобразование сигнала, а только вычисление фиксированных значений его автокорреляционной функции.

В качестве примера на рис. 6 представлены графики ожидаемого сигнала x(t, 1) и аддитивной смеси сигнала и шума n(t), единственно доступной для наблюдения. Нижний график на рис. 6 наглядно показывает, как сигнал почти полностью теряется на фоне шума.

Расчеты, реализуемые фильтром, дают при этом следующие значения выходного сигнала соответственно при наличии и отсутствии сигнала, подлежащего обнаружению:

 

 

При наличии сигнала () выходной сигнал корреляционного фильтра принимает значение 0,445, то есть примерно значение, равное половине квадрата амплитуды, а в условиях отсутствия сигнала () значение сигнала составляет всего-то -0,025.

На рис. 7 представлены графики изменения корреляционных функций шума (синяя линия) и смеси сигнала и шума (красная линия), рассчитанные в соответствии с данными, изображенными на рис. 6. Представленные кривые повторяют то, что было представлено на рис. 4, но соответствуют не только теоретическим выводам, но и практическим результатам расчетов.

Согласованная фильтрация

Согласованным называется фильтр, импульсная переходная функция которого является зеркальным отображением импульса, для обнаружения которого он и предназначен. Такой фильтр «согласован» с ожидаемым сигналом и предназначается для обнаружения сигнала только заранее известной формы.

Предположим, что нужно на фоне помех обнаруживать сигнал:

Сигнал изображен на рис. 8. Пропустим этот сигнал через фильтр с импульсной переходной функцией:

.

Функция является зеркальным отображением подлежащего обнаружению сигнала относительно прямой, проведенной параллельно оси ОХ через точку с абсциссой .

Сигнал на выходе фильтра определяется как свертка зашумленного входного сигнала и импульсной переходной функции:

Два последние интеграла с точностью до постоянного множителя определяют значения автокорреляционной функции сигнала и взаимной корреляционной функции сигнала и шума, разделенных промежутком времени :

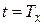Но если сигнал и шум не коррелируют, то и в момент времени выходной сигнал фильтра должен достигать наибольшего значения, равного .

Рассмотрим пример построения согласованного фильтра.

На фоне шума нужно обнаружить сигнал прямоугольной формы

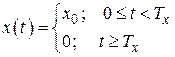
Согласованный фильтр должен обладать такой же импульсной переходной функцией:

Такую импульсную переходную функцию можно получить из двух функций единичного скачка в соответствии с рис. 9.

Передаточная функция фильтра получается преобразованием Лапласа импульсной переходной функции. Поэтому, отбрасывая постоянный множитель 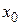, получаем выражение:

Полученное выражение говорит о том, что фильтр, согласованный с прямоугольным импульсом длительностью , должен состоять из звена задержки на время и интегрирующего звена. Структурная схема фильтра представлена на рис. 10.

Дифференциальное уравнение, описывающее работу фильтра, получается непосредственно из его передаточной функции:

где - предполагаемая длительность импульса.

На рис. 11 представлена реализация зашумленного сигнала z(t), в котором предполагается наличие прямоугольного импульса протяженностью 0,1 с.

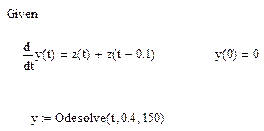Для обнаружения прямоугольного импульса в содержимом такого сигнала следует пропустить такой сигнал через согласованный фильтр при времени задержки =0.1 с или решить приведенное выше дифференциальное уравнение:

График выходного сигнала фильтра y(t) представлен на рис. 12.

При отсутствии шума выходной сигнал имел бы вид, который можно получить решением того же дифференциального уравнения при подстановке вместо z(t) искомого сигнала x(t). Тогда на выходе фильтра получился бы сигнал, представленный на рис. 13.

Схожесть сигналов на рис. 12 и 13 говорит о том, что сигнал на рис. 11 действительно содержит в себе прямоугольный импульс протяженностью в 0,1 с.

На рис. 14 представлена форма сигнала на выходе того же фильтра при отсутствии прямоугольного импульса на фоне тех же шумов. Форма сигнала существенно отличается от той, что была изображена на рис. 13. Это и позволяет утверждать, что сигнал не обнаружен.