Общие методические указания
При решении и оформлении задач необходимо соблюдать следующие требования:
1. Записать краткое условие задачи, выразить все известные величины в одной и той же системе единиц (как правило, в СИ). При необходимости ввести дополнительные постоянные физические величины.
2. Решение задач следует сопровождать краткими, но исчерпывающими объяснениями. При необходимости дать чертеж или график.
3. Решать задачу надо первоначально в общем виде, выразив искомую величину в буквенных обозначениях, заданных в условии задачи, затем произвести вычисления.
В конце каждой задачи дан ответ, кроме тех случаев, когда решение задачи предполагает только буквенное решение.
В течение семестра студенты выполняют две контрольные работы: первую – по механике, вторую – по молекулярной физике и термодинамике.
Результаты контроля аудиторной и самостоятельной работы студентов на практических занятиях учитываются лектором при приеме экзаменов и дифференцированных зачетов.
ЭЛЕМЕНТЫ КИНЕМАТИКИ
Основные законы и формулы
· Средняя и мгновенная скорости материальной точки
, 
,
где 
– перемещение точки за время 
, 
– радиус-вектор, определяющий положение точки.
· Для прямолинейного равномерного движения (
)
,
где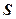 
– путь, пройденный точкой за время 
.
· Среднее и мгновенное ускорения материальной точки:
, 
.
· Полное ускорение при криволинейном движении:
, 
,
где 
– тангенциальная составляющая ускорения, направленная по касательной к траектории;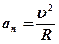 
– нормальная составляющая ускорения, направленная к центру кривизны траектории (
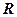– радиус кривизны траектории в данной точке).
· Путь и скорость для равнопеременного движения материальной точки (
):
; 
,
где 
– начальная скорость, «+» соответствует равноускоренному движению, «-» – равнозамедленному.
· Угловая скорость
.
· Угловое ускорение
.
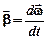· Угловая скорость для равномерного вращательного движения твердого тела
,
где 
– угол поворота тела; 
– период вращения; 
– частота вращения (
– число оборотов, совершаемых телом за время ).
· Угол поворота и угловая скорость для равнопеременного вращательного движения твердого тела (
):
; 
,
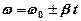где 
– начальная угловая скорость, «+» соответствует равноускоренному вращению, «-» – равнозамедленному.
· Связь между линейными и угловыми величинами:
; 
;
; 
где 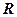– расстояние от точки до мгновенной оси вращения.
Задания
1.1. Пароход идет по реке от пункта А до пункта В со скоростью 10 км/ч, а обратно – со скоростью 16 км/ч. Найдите: 1) среднюю скорость парохода, 2) скорость течения реки. [12,3 км/ч; 0,83 м/с].
1.2. Скорость течения реки 3 км/ч, а скорость движения лодки относительно воды 6 км/ч. Определите, под каким углом относительно берега должна двигаться лодка, чтобы проплыть поперек реки. [60°].
1.3. Велосипедист проехал первую половину времени своего движения со скоростью 16 км/ч, вторую половину времени — со скоростью 12 км/ч. Определите среднюю скорость движения велосипедиста. [14 км/ч].
1.4. Велосипедист проехал первую половину пути со скоростью 16 км/ч, вторую половину пути – со скоростью 12 км/ч. Определите среднюю скорость движения велосипедиста. [13,7 км/ч].
1.5. Студент проехал половину пути на велосипеде со скоростью 16 км/ч. Далее в течение половины оставшегося времени он ехал со скоростью 12 км/ч, а затем до конца пути шел пешком со скоростью 5 км/ч. Определите среднюю скорость движения студента на всем пути. [11,1 км/ч].
1.6. После удара клюшкой шайба скользит по льду с постоянным ускорением. В конце пятой секунды после начала движения ее скорость была равна 1,5 м/с, а в конце шестой секунды шайба остановилась. С каким ускорением двигалась шайба, какой путь прошла и какова была ее скорость на расстоянии 20 м от начала движения? [1,5 м/c2; 27 м; 4,6 м/с].
1.7. Тело, брошенное вертикально вверх, через 3 с после начала движения имело скорость 7 м/с. На какую максимальную высоту относительно места броска поднялось тело? Считать 
. Сопротивлением воздуха пренебречь. [67,6 м].
1.8. Тело падает вертикально с высоты 19,6 м с нулевой начальной скоростью. Какой путь пройдет тело: 1) за первую 0,1 с своего движения, 2) за последнюю 0,1 с своего движения? Считать . Сопротивлением воздуха пренебречь. [0,049 м; 1,9 м].
1.9. Тело падает вертикально с высоты 19,6 м с нулевой начальной скоростью. За какое время тело пройдет: 1) первый метр своего пути, 2) последний метр своего пути? Считать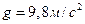 
. Сопротивлением воздуха пренебречь. [0,4 с; 0,05 с].
1.10. С башни в горизонтальном направлении брошено тело с начальной скоростью 10 м/с. Пренебрегая сопротивлением воздуха, определите для момента времени 
= 2 с после начала движения: 1) скорость тела; 2) радиус кривизны траектории. Считать 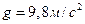. [22 м/с; 109 м].
1.11. Камень брошен горизонтально со скоростью 5м/с. Определите нормальное и тангенциальное ускорения камня через 1 с после начала движения. Считать 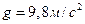. Сопротивлением воздуха пренебречь. [4,45 м/с2; 8,73 м/с2].
1.12. Камень брошен горизонтально со скоростью 10 м/с. Найдите радиус кривизны траектории камня через 3 с после начала движения. Считать 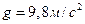. Сопротивление воздуха не учитывать. [305 м].
1.13. Материальная точка начинает двигаться по окружности радиусом 
= 2,5 см с постоянным тангенциальным ускорением 
=0,5 см/с2. Определите: 1) момент времени, при котором вектор ускорения 
образует с вектором скорости 
угол 45°; 2) путь, пройденный за это время движущейся точкой. [1) 
с; 2) 1,25 см]
1.14. Линейная скорость точки, находящейся на ободе вращающегося диска, в три раза больше, чем линейная скорость точки, находящейся на 6 см ближе к его оси. Определите радиус диска. [9 см].
1.15. Колесо вращается с постоянным угловым ускорением 3 рад/с2. Определите радиус колеса, если через 1 с после начала движения полное ускорение колеса 7,5 м/с2. [79 см].
1.16. Два автомобиля, выехав одновременно из одного пункта, движутся прямолинейно в одном направлении. Зависимость пройденного ими пути задается уравнениями 
и 
. Определите закон изменения относительной скорости автомобилей.
1.17. Кинематические уравнения движения двух материальных точек имеют вид 
и 
, где 
, 
, 
. Определите: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорения 
и 
для этого момента. [1) 0; 2) – 4 м/с2; 2 м/с2].
1.18. Диск вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, от времени задается уравнением 
(
= 0,3 м/с2, 
= 0,1 м/с3). Определите радиус, если к концу 2-й секунды движения вектор полного ускорения образует с вектором скорости угол 
= 86°. [0,1 м].
1.19. Нормальное ускорение точки, движущейся по окружности радиусом 
, задается уравнением 
, где =4 м/с4. Определите: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время 
=5 с после начала движения; 3) полное ускорение для момента времени 
= 1 с. [1)4 м/с2; 2)50 м; 3) 
м/с2].
1.20. Зависимость пройденного телом пути 
от времени выражается уравнением 
( = 2 м/с, = 3 м/с2, 
= 4 м/с3). Запишите выражения для скорости и ускорения. Определите для момента времени 
после начала движения пройденный путь, скорость и ускорение. [24 м; 38 м/с; 42 м/с2].
1.21. Зависимость пройденного телом пути от времени задаётся уравнением 
, где =5м, =4м/с, =1м/с2. Запишите выражения для скорости и ускорения. Определите для момента времени 
после начала движения пройденный путь, скорость и ускорение. [2м; 2м/с; 2 м/с2].
1.22. Зависимость пройденного телом пути от времени задаётся уравнением 
, где =0,1м, =0,1м/с, =0,14м/с2, 
=0,01м/с3. 1. Через сколько времени после начала движения ускорение тела будет равно 1м/с2? 2. Чему равно среднее ускорение тела за этот промежуток времени? [1) через 12с; 2) 0,64 м/с2].
1.23. Зависимость пройденного телом пути от времени задаётся уравнением , где =6м, =3м/с, =2м/с2. Найдите среднюю скорость и среднее ускорение в интервале времени от 1с до 4с. [ 
=7м/с; 
=4м/с2].
1.24. Зависимость пройденного телом пути по окружности радиусом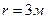 
задается уравнением 
( = 0,4 м/с2, = 0,1 м/с). Для момента времени 
после начала движения определите нормальное, тангенциальное и полное ускорения. [0,27 м/с2; 0,8 м/с2; 0,84 м/с2].
1.25. Радиус-вектор материальной точки изменяется со временем по закону 
, где 
- орты осей 
и 
. Определите для момента времени = 1 с модуль скорости и модуль ускорения. [6,7 м/с; 8,48 м/с2].
1.26. Радиус-вектор материальной точки изменяется со временем по закону 
. Запишите зависимости скорости и ускорения от времени. Определите модуль скорости в момент времени = 2 с. [16,3 м/с].
1.27. Диск радиусом 10 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением 
( =1 рад/с, =1 рад/с2, = 1 рад/с3). Определите для точек на ободе диска к концу второй секунды после начала движения тангенциальное, нормальное и полное ускорения. [1,4 м/с2; 28,9 м/с2; 28,9 м/с2].
1.28. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением 
( =0,5 рад/с2). Определите к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) для точки, находящейся на расстоянии 80 см от оси вращения, тангенциальное, нормальное и полное ускорения. [1) 2 рад/с; 2) 1 рад/с2; 3) 0,8 м/с2; 3,2 м/с2; 3,3 м/с2].
1.29. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением ( =0,1рад/с2). Определите полное ускорение точки на ободе диска к концу второй секунды после начала движения, если в этот момент линейная скорость этой точки 0,4 м/с. [0,25 м/с2].
1.30. Диск радиусом 0,2 м вращается вокруг неподвижной оси так, что зависимость угловой скорости от времени задается уравнением 
, где 
. Определите для точек на ободе диска к концу первой секунды после начала движения полное ускорение и число оборотов, сделанных диском за первую минуту движения. [5,8 м/c2; 15, 9].
1.31. Диск радиусом 10 см вращается так, что зависимость угла поворота радиуса диска от времени задается уравнением 
( = 2 рад, = 4 рад/с3). Определите для точек на ободе колеса: 1) нормальное ускорение в момент времени 2 с; 2) тангенциальное ускорение для этого же момента; 3) угол поворота, при котором полное ускорение составляет с радиусом колеса 45°. [1) 230 м/с2; 2) 4,8 м/с2; 3) 2,67 рад].
1.32. Якорь электродвигателя, имеющий частоту вращения 50 с-1, после выключения тока, сделав 628 оборотов, остановился. Определите угловое ускорение якоря. [12,5 рад/с2].
1.33. Колесо автомобиля вращается равнозамедленно. За время 2 мин оно изменило частоту вращения от 240 до 60 мин-1. Определите: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время. [1) 0,157 рад/с2; 2) 300].
1.34. Колесо, вращаясь равноускоренно, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найдите угловое ускорение колеса. [3,2 рад/с2].
1.35. Колесо спустя 1 мин после начала вращения приобретает скорость, соответствующую частоте 720 об/мин. Найдите угловое ускорение колеса и число оборотов, сделанных колесом за эту минуту. Движение считать равноускоренным. [1,26 рад/с2; 360].
1.36. Колесо, вращаясь равнозамедленно, при торможении уменьшило частоту вращения за 1 мин с 300 до 180 об/мин. Найдите угловое ускорение колеса и число оборотов, сделанных за это время. [ 0,21 рад/с2; 240].
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
