Биномиальный закон. Случайная величина 
называется распределенной по биномиальному закону, если она принимает конечное множество значений 0,1,… 
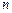, а вероятность того, что 
, выражается формулой: 
, где 
- вероятность наступления события А при одном испытании, 
.
Числовые характеристики биномиального закона распределения: 
, 
.
Закон Пуассона. Дискретная случайная величина называется распределенной по закону Пуассона, если она принимает счетное множество значений 0, 1, 2, …, 
, …, а вероятность того, что , выражается формулой: 
, где 
– параметр закона Пуассона. Числовые характеристики закона Пуассона: 
, 
. Опр. Интенсивностью потока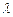 
наз-ют среднее число событий, которые появляются в единицу времени. Док-но, что если известна постоянная интенсивность потока 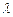, то вер-ть появления 
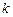событий за время длительностью 
определяется форм.: 
.
Равномерное распределение. Непрерывная случайная величина называется равномерно 
распределенной в интервале 
, если ее плотность распределения в этом интервале постоянна, а вне его равна нулю: 
Числовые характеристики равномерного закона распределения: 
, 
.
График дифференциальной функции равномерного распределения приведен на рис.
Нормальное распределение. Непрерывная случайная величина называется нормально распределенной, если ее плотность распределения равна 
, где - математическое ожидание, 
- среднее квадратическое отклонение. График дифференциальной ф-ии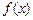 
нормального закона распределения (нормальная кривая или кривая Гаусса) на рис.
Вероятность того, что нормально распределенная случайная величина примет значение в интервале 
, выражается формулой: 
, где 
. Для нормального закона распределения верна следующая формула: 
.
Показательное распределение. Показательным называется распределение, дифференциальная функция которого имеет вид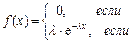 
где 
– параметр показательного распределения. График дифференциальной функции показательного распределения приведен на рис. Числовые характеристики показательного распределения: 
, 
. Интегральная функция для показательного распределения имеет вид 
. Функция надежности. Показательное расп-ешироко применяетсяв теории надежности. Пусть 
– продолжительность безотказной работы прибора. Ф-я распределения случайной величины Т выражает вероятность отказа за время t: 
. Опр. Функцией надежности 
наз-ют ф-ю, определяющую вероятность безотказной работы элемента за время длительностью : 
. Для показат. закона рас-я вер-ть безотказ. работы элемента за время 
выч-ся по формуле: 
, где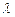 
- интенсивность отказов.
