1) Площадь криволинейной поверхности, уравнение которой z = f(x, y), можно найти в виде: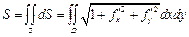 
(D – проекция S на плоскость О ху). 2) Масса поверхности 
3) Моменты поверхности: 
– статические моменты поверхности относительно координатных плоскостей O xy, O xz, O yz;
– моменты инерции поверхности относительно координатных осей;
– моменты инерции поверхности относительно координатных плоскостей;
– момент инерции поверхности относительно начала координат.
4) Координаты центра масс поверхности: 
.
§ 2. Поверхностный интеграл второго рода
Пусть в каждой точке некоторой поверхности 
определен непрерывный вектор 
. Зададим направление нормали 
к поверхности (эту сторону поверхности считаем положительной). Проекция 
вектора 
в каждой точке 
поверхности будет являться скаляром. Поэтому функция 
будет скалярной функцией и от нее можно вычислить поверхностный интеграл первого рода.
Опр. Поверхностным интегралом второго рода от вектора 
по поверхности называется поверхностный интеграл первого рода от проекции 
этого вектора на вектор нормали 
к и обозначается 
.
Т.к. 
и 
, то: 
– поверхностный интеграл второго рода общего вида
Зам. 1. Вычисление п оверхностного интеграла второго рода: 1) Если DXY, DXZ и DYZ - проекции поверхности S на координатные плоскости О ху, Oxz и Oyz, то
2) Если 
, то 
Аналогично, для 
и 
(сам-но).
Зам. 2. Связь между тройным интегралом по трехмерной области V и поверхностным интегралом 2-го рода по замкнутой поверхности S, ограничивающей тело V, задается формулой Гаусса-Остроградского: 
где запись «S+» означает, что интеграл, стоящий справа, вычисляется по внешней стороне поверхности S.
Зам 3. Формула Стокса устанавливает связь между поверхностным интегралом 2-го рода по поверхности σ и криволинейным интегралом 2-го рода по ограничивающему ее контуру L с учетом ориентации поверхности:
В теории поля поверхностный интеграл второго рода называется потоком векторного поля через поверхность.
Примеры потоков векторных полей: 1) Поток электрического поля точечного заряда напряженностью 
через замкнутую поверхность , охватывающую этот заряд, равен 
. 2) Поток магнитного поля с индукцией 
через поверхность равен 
.
Пример 1.
Найти массу поверхности 
с поверхностной плотностью γ = 2 z 2 + 3.
Решение.
На рассматриваемой поверхности 
Тогда
Проекцией D этой поверхности на координатную плоскость Оху является полукольцо с границами в виде дуг концентрических окружностей радиусов 3 и 4.
Применяя формулу и переходя к полярным координатам, получим:
