В радиотехнике в качестве базиса ортогональных функций берутся гармонические функции, что связано с простотой их генерации, а также с тем, что эти сигналы инвариантны относительно преобразований в стандартных электрических цепях.
Спектральное разложение сигнала – это представление сигнала в виде суммы гармонических колебаний с различными частотами.
Частотный спектр (спектр) – набор отдельных гармонических компонент сигнала.
2.3.1 Ряд Фурье
Ряд Фурьедля периодического сигнала (в ортонормированном базисе гармонических функций с учетом (15),(16)):

| (17) |
С коэффициентами:

| (18) |
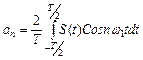
| (19) |

| (20) |
В общем случае периодический сигнал содержит постоянную составляющую и бесконечный набор гармонических колебаний – гармоник, с частотами wn = nw1, n = 0, 1,. кратными основной частоте (w1) последовательности. Четный сигнал имеет только косинусоидальные составляющие, нечетный сигнал – синусоидальные.
Каждую гармонику можно описать ее амплитудой Аn и начальной фазой jn. Тогда коэффициенты ряда Фурье:

| (21) |
и эквивалентная форма ряда Фурье:

| (22) |
Спектральная диаграмма периодического сигнала – это графическое изображение коэффициентов ряда Фурье для конкретного сигнала.
Спектральные диаграммы бывают амплитудные и фазовые (рис. 19). По горизонтальной оси диаграмм в масштабе откладываются частоты гармоник, а по вертикальной – их амплитуды или начальные фазы.

|
| Рис. 19. Амплитудная и фазовая диаграммы периодического сигнала |
2.3.2. Комплексная форма ряда Фурье
Спектральное разложение периодического сигнала можно провести в системе базисных функций, состоящих из экспонент с мнимыми показателями. Функции этого базиса периодичны с периодом Т и ортонормированны на отрезке времени [-T/2,T/2]. Тогда комплексный ряд Фурье с учетом нормы комплексного сигнала:

| (23) |
При вычислениях нужно учитывать связь экспоненциальных функций с тригонометрическими:

| (24) |

| (25) |

| (26) |
В случае экспоненциального представления спектр сигнала будет содержать гармоники в отрицательной области на оси частот, при этом нужно учитывать, что отрицательная частота это не физическое, а математическое понятие, определяемое представлением комплексных чисел.
2.3.3. Спектральное представление непериодических сигналов
Пусть существует одиночный импульсный сигнал S(t) конечной длительности. Мысленно дополним его такими же сигналами, периодически следующими через некоторые интервалы времени – Т. В результате получим периодическую последовательность Sпер(t), которую можно представить в виде ряда Фурье (23).
Для перехода к одиночному импульсу увеличим до бесконечности период повторения импульсов Т. При этом:
1) Частоты nw1 и (n+1)w1 окажутся сколь угодно близкими и поэтому дискретную переменную nw1 можно заменить непрерывной – w – текущей частотой.
2) Амплитудные коэффициенты Сn станут бесконечно малыми (стремящимися к нулю) из-за наличия Т®¥ в знаменателе.
3) Рассмотрим интервал частот Dw®0 в окрестностях некоторой частоты w0. В пределах этого интервала будет содержаться N отдельных пар спектральных составляющих, частоты которых будут отличаться друг от друга сколь угодно мало (N=Dw/w1=DwT/2p ).
4) В результате указанных предположений спектральные составляющие можно складывать так, как будто они имеют одну и ту же частоту и характеризуются одинаковыми комплексными амплитудами. Комплексная амплитуда эквивалентного гармонического сигнала внутри интервала Dw:
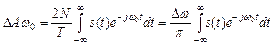
| (27) |
Причем величина

| (28) |
называется спектральной плотностью сигнала S(t) (спектральной функцией или преобразованием Фурье данного сигнала).
С точки зрения физического смысла спектральная плотность S(w0)=S(2pf0) – масштабный множитель, связывающий малую длину интервала частот Df и отвечающую ему комплексную амплитуду DAf0 гармонического сигнала на центральной частоте f0.
При решении обратной задачи, то есть нахождения сигнала по его спектральной плотности, необходимо воспользоваться обратным преобразованием Фурье для сигнала S(t):

| (29) |
Условие существования спектральной плотности сигнала: для того, чтобы сигналу S(t) можно было бы сопоставить его спектральную плотность S(w),необходимо, чтобы сигнал был абсолютно интегрируем, то есть, чтобы существовал интеграл:
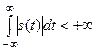
| (30) |
Кратко изложенная теория спектрального анализа сигналов позволяет анализировать прохождение сигналов через радиотехнические цепи, устройства, системы.
Модулированные сигналы
Сигналы, поступающие из источника сообщений (микрофона, передающей телевизионной камеры и т. д.), как правило, не могут быть переданы по радиоканалу на большие расстояния. Данное обстоятельство связано с тем, что эти сигналы являются низкочастотными и маломощными.
При передаче по радиоканалу необходимо спектры этих сигналов перенести из низкочастотной области в область более высоких частот (радиочастот). Данная процедура в радиотехнике носит название модуляции.
Остановимся более подробно на понятии несущего колебания. Несущее или высокочастотное колебание генерируется в передающем устройстве. В радиотехнике широкое распространение получили системы модуляции, в которых в качестве несущего используется простое гармоническое колебание s(t)=Sm ·Sin(w0t+j0). В результате изменения во времени одного из параметров несущего колебания (амплитуды, частоты, фазы) по закону передаваемого сообщения, несущее колебание приобретает новое свойство – нести в себе информацию, которая первоначально была заложена в сообщении. То есть, модуляция – процесс изменения одного из параметров (амплитуды, частоты, фазы) высокочастотного (несущего) колебания по закону управляющего низкочастотного колебания.
2.4.1. Амплитудная модуляция (АМ)
Процесс изменения во времени амплитуды несущего колебания по закону управляющего при неизменных частоте и фазе называется амплитудной модуляцией несущего колебания.
Аналитическое представление АМ сигнала:
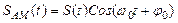
| (31) |
Иначе говоря, АМ – сигнал – это произведение огибающей S(t) и гармонического заполнения Cos(w0t+j0), причем на практике огибающая изменяется во времени гораздо медленнее, чем заполнение. Осциллограмма АМ – сигнала симметрична относительно горизонтальной оси. Связь межу несущей и огибающей в АМ – сигнале определяется в общем виде как:

| (32) |
где S(t) – амплитуда несущего колебания без модуляции, М – коэффициент модуляции, Sупр(t) – управляющее колебание.
Величина М определяет глубину амплитудной модуляции. При малой глубине относительное изменение величины огибающей невелико: МSупр(t)<<1. Применение АМ – сигналов с малой глубиной модуляции нецелесообразно по причине неполного использования мощности передатчика. При увеличении глубины модуляции до МSупр(t)>1 возникает перемодуляция, то есть искажается форма модулирующего сигнала.
Однотональная амплитудная модуляция – это частный случай АМ, когда управляющим является также гармоническое колебание с частотой W<w. Пример осциллограммы однотонального АМ – колебания при МSупр(t)=1 приведен на рис. 20,при МSупр(t)>1 – на рис. 21.

|
| Рис. 20. Осциллограмма однотонального АМ колебанияпри МSупр(t)=1 |
2.4.2. Угловая модуляция
При угловой модуляции по закону управляющего колебания изменяется частота или фаза несущего, а амплитуда остается неизменной.
Для гармонического колебания s(t) = SmSin(w0t + j0) = SmSiny(t) набег фазы за какой-либо конечный промежуток времени от t=t1 до t=t2 равен y(t2) - y(t1) = (w0t2 + j0) - (w0t1+j0) = w0(t2 - t1). При постоянной угловой частоте набег фазы за какой-либо промежуток времени пропорционален длительности этого промежутка.
Угловую частоту можно определить как w0={y(t2) - y(t1)}/{t2-t1}, то есть угловая частота – это скорость изменения фазы колебания.

|
| Рис. 21. Осциллограмма однотонального АМ колебанияпри МSупр(t)=1.4 |
Переходя к сложному колебанию, частота которого может изменяться во времени необходимо перейти к дифференциальным и интегральным соотношениям:
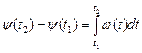
| (33) |

| (34) |
Из (33), (34) следует, что полная фаза высокочастотного колебания в момент t:
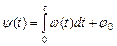
| (35) |
Итак, в общем виде выражение для высокочастотного колебания, амплитуда которого постоянна, а аргумент y(t) модулирован:

| (36) |
Соотношения (34), (35), устанавливающие связь между изменениями частоты и фазы, указывают на общность двух разновидностей угловой модуляции. Рассмотрим пример простейшей гармонической ЧМ, когда мгновенная частота определяется как:

| (37) |
где wД = 2pfД – амплитуда частотного отклонения или девиация частоты (или просто девиация); w0 – несущая, W – модулирующая частоты.
Подставим (37) в (35):
 . .
| (38) |
Проинтегрировав, подставим в (36):

| (39) |
Полученное модулированное колебание можно рассматривать и как модулированное по фазе, закон этой модуляции является интегральным по отношению к закону изменения частоты.
Таким образом, модуляция частоты несущего колебания по закону wДCosWt приводит к модуляции фазы по закону ( wД/W)SinWt. Амплитуду изменения фазы называют индексом угловой модуляции (40).
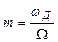
| (40) |
Пример осциллограммы с однотональной ЧМ приведен на рис. 22.

|
| Рис. 22. Осциллограмма однотонального ЧМ колебания |
3. Прохождение детерминированных сигналов через линейные стационарные цепи с сосредоточенными параметрами
Любое радиотехническое устройство представляет собой систему, то есть совокупность физических объектов, между которыми существуют определенные взаимодействия.
В системе можно выделить вход, на который подается исходный сигнал, и выход, откуда снимается преобразованный сигнал.
Если интересует только связь между входными и выходными сигналами и не рассматривают внутренние процессы в системе, то систему рассматривают как «черный ящик» (рис. 23).

|
| Рис. 23. Система как «черный ящик» |
Закон связи между входным сигналом Uвх(t) и выходным сигналом (откликом, выходной реакцией системы) Uвых(t) задается системным оператором Т:

| (41) |
При исследовании необходимо указывать и область допустимых входных Dвх и выходных Dвых воздействий, которые описывают характер сигналов (непрерывных, дискретных, детерминированных, случайных и т. д.).
Математической моделью (ММ) системы называют совокупность системного оператора Т и областей допустимых сигналов Dвх, Dвых.
На основании свойств ММ можно проводить классификацию систем.
Классификация систем
2.1.1. Стационарные и нестационарные системы
Система стационарна, если ее выходная реакция не зависит от того, в какой момент времени поступает входной сигнал при любом значении t0.

| (42) |
Если система не инвариантна относительно выбора начала отсчета времени (не выполняются равенства (41,42)), то такая система называется нестационарной (системой с переменными во времени параметрами или параметрической).
3.1.2. Линейные и нелинейные системы
Данный принцип классификации основан на различной реакции системы на сложный суммарный сигнал.
Если оператор системы:

| (43) |

| (44) |
где a – произвольное число, то такая система называется линейной.
Система линейная, если выполняются условия (43,44), то есть выполняется фундаментальный принцип суперпозиции.
Если принцип суперпозиции не выполняется, то система нелинейная.
3.1.3. Сосредоточенные и распределенные системы
Классификация основана на сопоставлении физических размеров системы и рабочей длины волны.
Если характерный размер системы (наибольшая длина соединительных проводников цепи) много меньше длины волны, то такая радиотехническая система является системой с сосредоточенными параметрами. В такой системе можно выделить физические области локализации электрического (конденсатор) и магнитного (катушка индуктивности) полей. Для описания таких систем используют ММ – принципиальные схемы. Область применения сосредоточенных систем до сотен МГц.
В диапазоне СВЧ размеры системы соизмеримы с длиной волны передаваемых колебаний, поэтому необходимо учитывать время распространения сигнала, такие системы называют системами с распределенными параметрами.






