2.1.1. Детерминированные и случайные сигналы
Детерминированный сигнал – это сигнал, мгновенное значение которого в любой момент времени можно предсказать с вероятностью равной единице.
Примером детерминированного сигнала (рис.10) могут быть: последовательности импульсов (форма, амплитуда и положение во времени которых известны), непрерывные сигналы с заданными амплитудно-фазовыми соотношениями.
Способы задания ММ сигнала: аналитическое выражение (формула), осциллограмма, спектральное представление.
Пример ММ детерминированного сигнала.
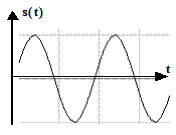
s(t)=Sm ·Sin(w0t+j0)
| 

| ||||
| Рис. 10. Детерминированный (гармонический) синусоидальный сигнал |
Случайный сигнал – сигнал, мгновенное значение которого в любой момент времени заранее неизвестно, а может быть предсказано с некоторой вероятностью, меньше единицы.
Примером случайного сигнала (рис. 11) может быть напряжение, соответствующее человеческой речи, музыке; последовательность радиоимпульсов на входе радиолокационного приемника; помехи, шумы.
2.1.2. Сигналы, применяемые в радиоэлектронике
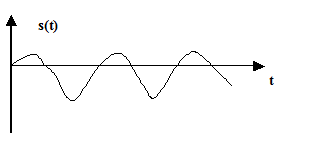
Непрерывные по величине (уровню) и непрерывные по времени (непрерывные или аналоговые) сигналы – принимают любые значения s(t) и существуют в любой момент в заданном временном интервале (рис. 12).
|
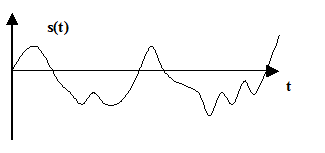
| Рис. 11. Случайный процесс |
|
| Рис. 12. Аналоговый сигнал |
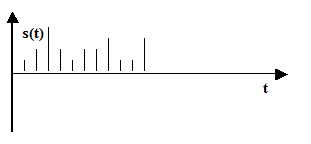
Непрерывные по величине и дискретные по времени сигналы заданы при дискретных значениях времени (на счетном множестве точек), величина сигнала s(t) в этих точках принимает любое значение в определенном интервале по оси ординат.
Термин «дискретный» характеризует способ задания сигнала на оси времени (рис. 13).
|
| Рис. 13. Непрерывный по величине и дискретный по времени сигнал |
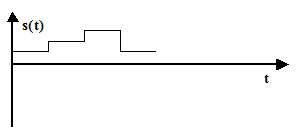
Квантованные по величине и непрерывные по времени сигналы заданы на всей временной оси, но величина s(t) может принимать лишь дискретные (квантованные) значения (рис. 14).
|
| Рис. 14. Квантованный по величине и непрерывный по времени сигнал |
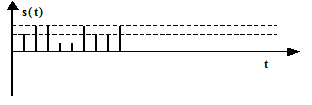
Квантованные по величине и дискретные по времени (цифровые) сигналы – передаются значения уровней сигнала в цифровой форме (рис. 15).
|
| Рис. 15. Цифровой сигнал |
2.1.3. Импульсные сигналы
Импульс – колебание, существующее лишь в пределах конечного отрезка времени. На рис. 16 и 17 представлены видеоимпульс и радиоимпульс.
|
| Рис. 16. Видеоимпульс |
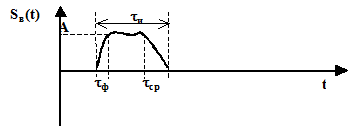
Для трапециидального видеоимпульса вводят параметры:
А – амплитуда;
tи – длительность видеоимпульса;
tф – длительность фронта;
tср – длительность среза.
|
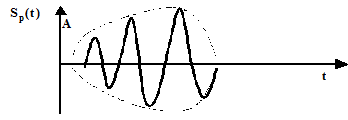
| Рис. 17. Радиоимпульс |
Sр(t)=Sв(t)Sin(w0t+j0)
Sв(t) – видеоимпульс – огибающая для радиоимпульса.
Sin(w0t+j0) – заполнение радиоимпульса.
2.1.4. Специальные сигналы
Функция включения (единичная функция (рис. 18) или функция Хевисайда) описывает процесс перехода некоторого физического объекта из «нулевого» в «единичное» состояние, причем этот переход совершается мгновенно.
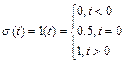
| (1) |
C помощью функции включения удобно описывать разнообразные процессы коммутации в электрических цепях.
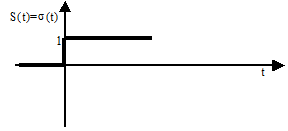
|
| Рис. 18. Функция включения |
Дельта-функция (Функция Дирака) является импульсом, длительность которого стремится к нулю, при этом высота импульса неограниченно возрастает. Принято говорить, что функция сосредоточена в этой точке.
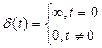
| (2) |

| (3) |






