ХОДОВ
ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ
Координаты пунктов могут быть определены проложением через них теодолитных ходов, опирающихся в начале и в конце хода на пункты с известными координатами и стороны с известными дирекционными углами. При математической обработке результатов таких измерений координаты определяемых пунктов получают однозначно, а их точность зависит от точности полевых измерений, точности исходных данных и принятого метода обработки измерений.
На практике возможно появление ситуаций, когда в геодезических построениях возникает неоднозначность получения определяемых величин, например координат пунктов.
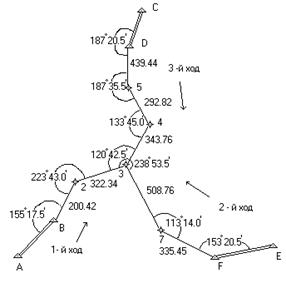
С этой точки зрения рассмотрим геодезическое построение в виде системы трех теодолитных ходов с одной узловой точкой (рис. 4.1). Практическая необходимость построения такой системы обусловлена невозможностью определения положения пунктов путем проложения через них одного теодолитного хода (например, из-за отсутствия на местности необходимых видимостей). Ограничивающим фактором может быть превышение допустимой длины одиночного теодолитного хода или нарушение каких-либо других нормативных требований.
В системе теодолитных ходов, показанных на рис. 4.1, положение пунктов определено от трех исходных - B, D, F, тогда как для этой цели достаточно было двух из них. Следовательно, в сети имеются избыточные измерения (избыточные в смысле их необходимого числа при безконтрольном определении координат пунктов). Эта избыточность и приводит к неоднозначности решения. Так, например, координаты любого определяемого пункта сети, показанной на рис.4.1, могут быть получены, как минимум, дважды. В таком случае говорят о необходимости уравнивания.
|
Рис.4.1
Примечание: на рис. представлены данные, которые должны быть изменены в соответствии с вариантом (см. табл. 4.2).
Способы уравнивания разделяются на строгие, когда уравнивание производится под условием минимума суммы произведений квадратов поправок в измеренные величины, и нестрогие (раздельные), когда сначала уравнивают углы, а затем раздельно между собой приращения координат.
При выборе способа уравнения исходят прежде всего из необходимой точности получения координат пунктов. Если раздельное уравнивание обеспечивает указанное требование, то его применение в настоящее время предпочтительно, т. к. упрощает процесс вычислений. Последний может быть выполнен как посредством традиционных средств, так и с помощью микрокалькуляторов или ЭВМ.
При раздельном уравнивании системы теодолитных ходов с одной узловой точкой уравнивают сначала измеренные углы, а затем по полученным вероятнейшим значениям дирекционных углов и измеренным горизонтальным проложениям линий вычисляют приращения координат, которые уравнивают отдельно, приращения по оси абсцисс и приращения по оси ординат.
ИСХОДНЫЕ ДАННЫЕ
Вычислить координаты пунктов системы теодолитных ходов с одним узловым пунктом.
Таблица 4.1