Дифференциальными уравнениями (д. у.) 1-го порядка называются уравнение вида F(x, у, у¢) = 0 (1)
или у¢ = f(x, у), что можно записать и так (1¢)
dу = f(x,у)dx. (1¢¢)
Обозначим через Д область существования решения (1) - (1¢¢).
Общим решением д.у. (1) - (1¢¢) называется функция у =  , (2)
, (2)
где С - произвольная константа, удовлетворяющая условиям:
а) она является решением д.у. при любом С;
б) при любых начальных условиях 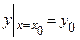 . (*)
. (*)
 , найдется такое значение С = С0, что функция
, найдется такое значение С = С0, что функция 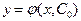
удовлетворяет условиям (*).
Нахождение такого С = С0 по условиям (*) называется решением задачи Коши. Найденная таким образом функция 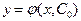 называется иначе частным решением д.у.
называется иначе частным решением д.у.
Если решение д.у. найдено в виде Ф(х, у, С) =0, оно называется общим интегралом этого уравнения.
Д.у. с разделяющимися переменными.
Общий вид: m1(x) * m2(y) dx + n1(x) * n2(y)dx = 0, (m2(y) ¹ 0 и n1(x) ¹ 0). (3)
Разделим переменные: 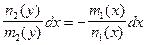 . Тогда
. Тогда 
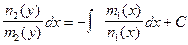 является общим интегралом уравнения (3)
является общим интегралом уравнения (3)
2) Однородные д.у.
Общий вид: у¢ = f(x,y), (4)
где f(x,y) - однородная функция “нулевого измерения”, что означает выполнение условия f(tx,ty) = f(x,y) для любого t. (4) может быть приведено к виду (4¢):
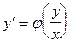 . (4¢)
. (4¢)
Подставной у = u * x приводится к уравнению с разделяющимися переменными: y¢ = u¢x + u.
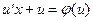 ;
; 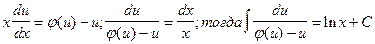 -
-
общий интеграл уравнения (4).
Линейное д.у. 1-го порядка.
Общий вид:
у¢ + Р(х) * у = Q (х). (5)
Подстановка y = u * V, где u = u(x), V = V(x); y¢ = u¢V + uV¢.
u¢V + uV¢ + P(x) * uV = Q(x). (5¢)
Выберем V так, чтобы V¢ + P(x) * V = 0. Это - д.у. с разделяющимися переменными.
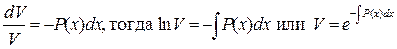 , тогда (5¢) будет иметь вид:
, тогда (5¢) будет иметь вид:
u¢V = Q (x), а это также д.у. с разделяющимися переменными (V уже найдено!):  интегрируя, получим:
интегрируя, получим: 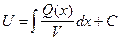 .
.
Окончательно,  . Общий вид (5).
. Общий вид (5).
4) Уравнение Бернулли.
Общий вид: y¢ + P(x) * y = Q(x) * yn (6)
(n ¹ 0 и n ¹ 1). Метод решения - такой же, как линейного уравнения (5).
ЗАДАЧА № 1
1.  ; 2.
; 2. 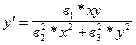 ;
;
3. 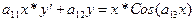 ; 4.
; 4.  .
.
1.  .
.
Переменные разделились.
Тогда  ;
; 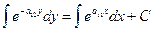 .
.
Закончить самостоятельно.
2. После замены у = t * x, у¢ = t¢x + t имеем:
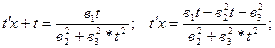
учитывая, что 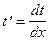 ,
,

Интеграл слева вычислить самостоятельно.
3. 
Это - линейное уравнение, где 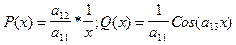 ,
,
у = U * V, y¢ = U¢V + UV¢,
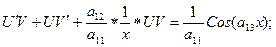
 - уравнение с разделяющимися переменными. Т. к.
- уравнение с разделяющимися переменными. Т. к.  то
то 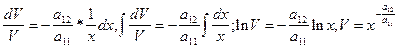 ;
;
 - уравнение с разделяющимися переменными.
- уравнение с разделяющимися переменными.
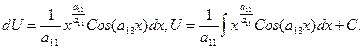 Окончательно,
Окончательно,
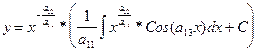 - общий интеграл исходного уравнения (последний интеграл вычислить самостоятельно).
- общий интеграл исходного уравнения (последний интеграл вычислить самостоятельно).

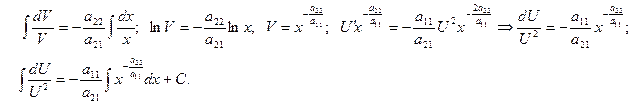
Далее по той же схеме, что и в предыдущем примере (закончить самостоятельно).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 2-ГО ПОРЯДКА
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Общий вид:
F(x, y, y¢, y¢¢) = 0 (7)
или
y¢¢ = f (x, y, y¢). (7¢)
Начальные условия имеют вид
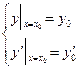 . (8)
. (8)
Функция 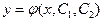 (9) называется общим решением (7) или (7¢) в соответствующей области Д (С1,С2 - произвольные константы), если при соответствующем выборе С1 и С2 эта функция дает частное решение (7), удовлетворяющее (8).
(9) называется общим решением (7) или (7¢) в соответствующей области Д (С1,С2 - произвольные константы), если при соответствующем выборе С1 и С2 эта функция дает частное решение (7), удовлетворяющее (8).
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 2-ГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
ОДНОРОДНЫЕ УРАВНЕНИЯ
Общий вид:
у¢¢ + а1у¢ + а2у = 0. (13)
Составляем характеристическое уравнение:
к2 + а1к + а2 = 0. (13¢)
Пусть к1, к2 - его корни. Возможны 3 случая:
а) корни вещественные, различные;
б) корни вещественные, равные: к1 = к2 = к (2-кратный корень);
в) корни комплексные, сопряженные к1,2 = а ± iв, где i =  ).
).
Вид общего решения (13) в каждом из этих случаев запишем в табл. 1.
Таблица 1
| Корни к1, к2 | Общее решение (13) ( ) )
|
| (а) |  . .
|
| (б) |  . .
|
| (в) |  . .
|
ЗАДАЧА № 2
1. у¢¢ - 4а112 у¢ + 3а111у = 0; 2. у¢¢ + 2а22 у¢ + а222у = 0;
3. у¢¢ + а21у¢ = 0; 4. у¢¢ + а332у = 0.
1. Характеристическое уравнение:  .
.
Легко находим, что к1 = 3а11, к2 = а11 (корни вещественные, различные). Это 1-й случай табл. 1. Тогда 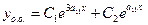 - общее решение.
- общее решение.
2. Характеристическое уравнение: 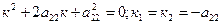 .
.
Далее применить табл. 1 и самостоятельно записать уо.о..
3. Характеристическое уравнение:  .
.
Закончить пример самостоятельно.
4. Характеристическое уравнение:  .
.
Закончить пример самостоятельно.
В следующих примерах найти частные решения д. у. (уч.о.), удовлетворяющие заданным начальным условиям.
5. у¢¢ - 3а12 у¢ + 2а12у = 0, у(1) = в1, у¢(1) = в2;
6. у¢¢ - а222у = 0, у(0) = в2, у¢(0) = в3.
5. Характеристическое уравнение:
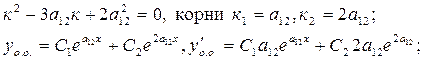

Решить систему, найти С1, С2 и уч .о..
6. Характеристическое уравнение:
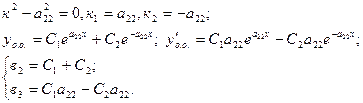
Решить систему, найти С1, С2 и уч.о..
НЕОДНОРОДНЫЕ УРАВНЕНИЯ






