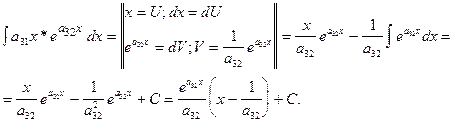ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Методические указания и
Контрольные задания № 3, 4
Для студентов заочной формы обучения
Ростов-на-Дону
2012 г.
УДК 517.5 (08)
Интегральное исчисление. Дифференциальные уравнения. - Ростов-на-Дону: РГСУ, 2012.- 32 c.
Методические указания содержат методы решения заданий из контрольных работ № 3, 4. Приведены необходимые теоретические сведения. Изложение сопровождается подробным решением типичных примеров.
Предназначены для студентов заочной формы обучения специальности ЗПГС, ЗИСС.
Составители: Богданов А.Е.
Корабельников Г.Я.
Рецензент: Ляпин А.А.
Редактор Н.Е.Гладких
Темплан 2012 г., поз.
ЛР 020818 от Подписано в печать Формат 60х84/16
Бумага белая. Ризограф. Уч. – изд. л. 2,0. Тираж 50 экз. Заказ
Редакционно-издательский центр Ростовского государственного строительного университета
344022, Ростов н/Д, ул. Социалистическая, 162
ã РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ
СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ, 2012
КОНТРОЛЬНАЯ РАБОТА № 3
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
При изучении дифференцированного исчисления решалась следующая задача: дана функция F(x), найти ее производную F¢(x) (в дальнейшем производную F¢(x) будем обозначать f(x)). Интегральное исчисление решает задачу обратную: для непрерывной функции f(x) найти такую функцию F(x), производная которой была бы тождественно равна функции f(x). Функция F(x) называется первообразной,
f(x) - подынтегральной. Ясно, что если F¢(x) = f(x), то и [F¢(x) + C]¢ = f(x). Здесь
С - произвольная постоянная величина.
Определение:
Неопределенным интегралом 
называется функция F(x) + C, производная которой равна подынтегральной функции f(x), т.е.
= F(x) + C, если [F(x) + C]¢ = f(x).
Подынтегральное выражение f(x)dx есть дифференциал для всех первообразных, т.е. d[F(x) + C] = f(x)dx.
Из определения следует, что процесс нахождения неопределенного интеграла сводится к нахождению первообразной данной функции.
ПРИМЕР:
Пусть f(x) = х. Тогда 
= 1/2x2 + C.
Справедливость равенства легко проверить дифференцированием:
.
Вообще, используя таблицу производных, можно составить таблицу основных интегралов:
1. 
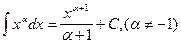
| 9. 
|
2. 
| 10. 
|
2¢. 
| 11. 
|
3.  
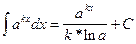
| 12. 
|
3¢. 
| 13. 
|
4. 
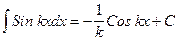
| 14.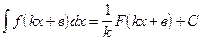 
|
5. 
| 15. 
|
6. 
| 16. 
|
7. 
| 17. 
|
8. 
| 18. 
|
ОСНОВНЫЕ СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
1. 
, т.е. знаки d и ò, стоящие перед некоторой функцией, друг друга уничтожают. Так 
.
2. 
, т.е. постоянный множитель можно выносить за знаки интеграла.
3. 
, т.е. неопределенный интеграл от суммы некоторых функций равен сумме интегралов от этих функций.
ПРИМЕР:
ЗАДАЧА № 1
Найти неопределенный интеграл 
.
= 
МЕТОД ПОДСТАНОВКИ
Метод заключается в том, что вместо переменной x вводят новую переменную, например t. Так, если положить х = j(t), то
Получаемый интеграл должен быть значительно проще данного. В противном случае следует искать другую форму введения новой переменной. Часто переменную t вводят так: t = j(x), а dt = j¢(x)dx. Это удобно, если данное подынтегральное выражение содержит дифференциал j¢(x)dx.
ПРИМЕР: 
Видно, что Cosx dx является дифференциалом для функции Sinx = t, Cosx dx = dt.
Получим 
(далее нужно вернуться к функции Sinx) 
ЗАДАЧА № 2
Найти неопределенный интеграл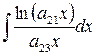 
.
= 
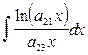ЗАДАЧА № 3
Найти неопределенный интеграл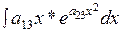 
.
.
ЗАДАЧА № 4
Найти неопределенный интеграл 
.
= 
ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ КВАДРАТНЫЙ ТРЕХЧЛЕН
В квадратном трехчлене ах2 + вх + С следует выделить полный квадрат:
.
ПРИМЕР:
ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ
Идея метода состоит в том, что подынтегральное выражение f(x)dx нужно представить в виде произведения U*dV, где U(x) и V(x) - дифференцируемые функции и воспользоваться формулой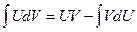 
.
При этом вновь полученный интеграл 
должен быть проще данного.
ЗАДАЧА № 5
Найти неопределенный интеграл 
.
= 
ЗАДАЧА № 6
Найти неопределенный интеграл 
.
= 
ЗАДАЧА № 7
Найти неопределенный интеграл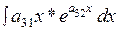 
.
