Леонардо да Вінчі
Сучасне твердження:
“Будь яка наука досягає значного
успіху, якщо використовує
у своєму розвитку математичні
методи і моделі”.
Вступ
Предмет математики
Кожна наука, яка вивчає ті чи інші явища оточуючого нас світу, має справу з притаманними їм величинами. Так, фізика – наука про найзагальніші форми руху матерії (механічної, теплової, електромагнітної та ін.) – торкається таких величин, як довжина, сила, температура, маса, питома вага, швидкість, прискорення, теплоємність, сила електричного струму та ін.
Незважаючи на надзвичайну різноманітність цих величин, всі вони мають одну спільну властивість: кожну величину можна виміряти, тобто порівняти з певною величиною тієї ж природи, взятою за одиницю міри. Так, довжина вимірюється одиницею довжини – метром, температура – одиницею температури – градусом, сила струму – ампером і т. д.
Абстрактне число, що його дістаємо внаслідок вимірювання конкретної величини одиницею масштабу, звуть вартістю, чи значенням величини, яка вимірюється. Якщо взяти будь-який закон природи, приміром закон Ленца-Джоуля про кількість виділюваного тепла при проходженні
електричного струму в провіднику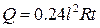 
, то він дає нам співвідношення між величинами, точніше співвідношення між числами, що виражають ці величини. Предметом дослідження математики і є якраз числа та різні співвідношення між ними, незалежно від того, які саме конкретні величини чи закони привели нас до цих чисел та їх співвідношень. Отже, абстрагуючись від індивідуальних властивостей тієї чи іншої конкретної величини і беручи до уваги тільки одну спільну властивість усіх величин, що про неї вже була мова, у математиці розглядають величину взагалі, і завдяки цьому створюють загальні теорії, застосовні до величин різноманітної природи.
Крім поняття числа із світу, який оточує людину, запозичено також поняття фігури. У світі існують різні речі, що мають певну форму і ці форми повинні були піддаватися порівнянню, перше ніж можна було дійти до поняття фігури. Враховуючи сказане, можна дати таке означення предмету математики: математика має за свій об’єкт просторові форми і кількісні співвідношення реального світу.
Як і в шкільному курсі (геометрії, алгебри, тригонометрії), так і в математичних дисциплінах вищої школи ці дві сторони – просторові форми і кількісні співвідношення – єдиної математики вимальовуються досить чітко і окреслено: аналітична геометрія вивчає просторові образи, диференціальне та інтегральне числення – кількісні співвідношення. Але за самим означенням, аналітична геометрія – це наука, що вивчає властивості геометричних образів засобами алгебри, тобто геометричні питання “перекладаються” на мову алгебри і зрештою зводяться до кількісних співвідношень, до певних обчислень. З другого боку, в диференціальному та інтегральному численні майже завжди вдаються до геометричного тлумачення тієї чи іншої теореми, користуючись поняттями аналітичної геометрії, та до застосувань до геометрії тих чи інших здобутих результатів. Глибокий взаємозв’язок геометрії й математичного аналізу та їх взаємопроникнення – характерна риса сучасної математики.
Число. Раціональні, ірраціональні та дійсні числа.
Основними поняттями сучасної математики є поняття числа, функції та границі. Хоча ці поняття мають багатовікову історію, яка іноді сягає в сиву давнину, але тільки в сучасній математиці вони набули характерної для них форми і стали наріжними каменями її будови.
Рахуючи окремі предмети, дістають так звані натуральні числа 1, 2, 3, 4,...
Вимірюючи ту чи іншу фізичну величину (час, довжину, температуру та ін.), дістають знову ж таки число. Воно може бути цілим, якщо величина, взята за одиницю масштабу, міститься у вимірюваній величині ціле число разів; дробовим, якщо існує інша менша одиниця, яка міститься ціле число разів як у вимірюваній величині, так і в обраній раніше більшій одиниці; і у цьому разі кажуть, що розглядувана величина спільномірна з одиницею міри. Нарешті, число буде ірраціональним, коли вимірювана величина неспільномірна з одиницею міри.
Розв’язання алгебраїчних задач викликало до життя у свій час (16 століття) від’ємні числа (цілі та дробові). Ще раніше (9 століття) індійці запровадили число нуль (санскритською мовою – “пустий”).
Цілі та дробові числа, як додатні, так і від’ємні разом з числом нуль звуть раціональними числами. Будь-яке раціональне число можна подати у вигляді нескоротного дробу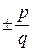 
, де p і q – натуральні числа. Наприклад:
; 
; 
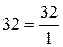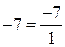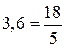
(дріб 
відноситься до нескоротних дробів).
Арифметичні дії над раціональними числами – додавання, віднімання, множення та ділення – завжди дають раціональне число. Ділення на нуль неприпустиме. Для практичних потреб (ліку, вимірювання, зважування та ін.) раціональних чисел цілком досить. Але в математиці та її застосуваннях обмежитись раціональними числами неможливо. Так, обчислюючи діагональ квадрата, сторона якого дорівнює 1, дістаємо число 
, відсутнє серед раціональних чисел. Немає такого раціонального дробу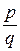 
(p і q – натуральні числа) квадрат якого дорівнював би 2. Справді, припустимо супротивне, а саме: що існує такий дріб 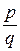, що 
. Дріб 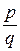вважаємо за нескоротний (у противному разі зробили б скорочення!). З рівності 
маємо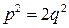 
, тобто p є число парне 
. Підставляючи цю вартість p, дістанем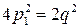о 
або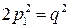 
. Звідси випливає, що й 
, а отже й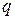 
- число парне. Виходить, що p і q мають спільник дільник 2, а це суперечить припущенню, що дріб 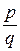- нескоротний. Отже, не існує раціонального дробу, квадрат якого дорівнює 2.
Таким чином, якщо обмежитися лише раціональними числами, то у геометрії не всім відрізкам можна було б приписати довжину, а в алгебрі просте рівняння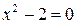 
, чи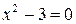 
не мало б кореня. Про факт, щойно наведений з геометрії, кажуть, що діагональ квадрата неспільномірна з його стороною (довжина якої дорівнює одиниці). Можна було б навести багато фактів, які настирливо вимагали розширення поняття числа. Це розширення досягнуто запровадженням у математику (поряд з раціональними числами) ірраціональних чисел. До них належать, наприклад, числа , 
, 
, 
, 
, 
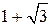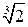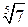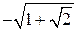та безліч інших.
З арифметики відомо що будь-яке раціональне число 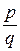можна завжди виразити через скінченний десятковий дріб, або через нескінченний десятковий періодичний, або мішаний періодичний. Приміром, 
; 
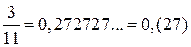. І, навпаки, будь-який періодичний десятковий дріб за відомими правилами, перетворюється у звичайний. Принципова відміна ірраціональних чисел від раціональних полягає у тому, що будь-яке ірраціональне число зображується нескінченним неперіодичним десятковим дробом.
