Состояние газа может быть охарактеризовано тремя величинами – давлением 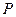 , объемом
, объемом  и температурой
и температурой 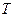 . Уравнение, связывающее эти величины, называется уравнением состояния вещества. В случае идеального газа таким уравнением является уравнение Менделеева-Клапейрона, которое для одного моля газа имеет вид:
. Уравнение, связывающее эти величины, называется уравнением состояния вещества. В случае идеального газа таким уравнением является уравнение Менделеева-Клапейрона, которое для одного моля газа имеет вид:
 (1)
(1)
где 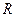 - универсальная газовая постоянная.
- универсальная газовая постоянная.
Молярная теплоемкость газа определяется количеством теплоты, которое необходимо сообщить 1 молю газа для нагревания его на 1 градус Кельвина.
Величина молярной теплоемкости газов зависит от условий нагревания. Для выяснения такой зависимости воспользуемся уравнением состояния (1) и первым началом термодинамики, согласно которому количество теплоты  , переданное системе (газу), затрачивается на увеличение её внутренней энергии
, переданное системе (газу), затрачивается на увеличение её внутренней энергии  и на работу
и на работу  , совершаемую системой (в данном случае газом) против внешних сил:
, совершаемую системой (в данном случае газом) против внешних сил:
 (2)
(2)
Следовательно, по определению молярной теплоемкости:
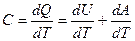 (3)
(3)
Из выражения (3) следует, что теплоемкость может иметь различные значения в зависимости от способов нагревания газа, так как одному и тому же значению  могут соответствовать различные значения
могут соответствовать различные значения  и
и  . Элементарная работа
. Элементарная работа  , согласно [1], равна
, согласно [1], равна  .
.
Из основного уравнения молекулярно-кинетической теории идеального газа известно, что среднее значение кинетической энергии поступательного движения одной молекулы [2]:
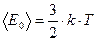 , (4)
, (4)
где  - постоянная Больцмана.
- постоянная Больцмана.
Кинетическая энергия многоатомных молекул зависит от числа степеней свободы, которое обозначается буквой  . Число степеней свободы – число независимых координат полностью определяющих положение системы (в данном случае молекулы) в пространстве.
. Число степеней свободы – число независимых координат полностью определяющих положение системы (в данном случае молекулы) в пространстве.
Согласно теореме Больцмана на каждую степень свободы молекулы приходится одинаковое значение энергии. Средняя энергия произвольной молекулы идеального газа [2]:
 . (5)
. (5)
Так как в идеальном газе потенциальной энергией молекул пренебрегают, то внутренняя энергия одного моля идеального газа определяется только кинетической.
 ,
,
где  - число Авогадро,
- число Авогадро, 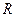 - универсальная газовая постоянная (
- универсальная газовая постоянная (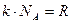 ).
).
Дифференциал от внутренней энергии:
 (6)
(6)
Рассмотрим основные процессы, протекающие в идеальном газе при изменении температуры, когда масса газа остается неизменной и равна одному молю.
1. Изохорический процесс. Процесс называется изохорическим, если объем газа при изменении температуры остается неизменным, т.е.  . В этом случае
. В этом случае  , работа газа также равна нулю (
, работа газа также равна нулю ( ), а подводимая к газу теплота идет только на увеличение его внутренней энергии. В таком случае из уравнения (3)
), а подводимая к газу теплота идет только на увеличение его внутренней энергии. В таком случае из уравнения (3)  , а с учетом (6) молярная теплоемкость при постоянном объеме:
, а с учетом (6) молярная теплоемкость при постоянном объеме:
 (7)
(7)
2. Изобарический процесс. Процесс, протекающий при постоянном давлении (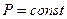 ), называется изобарическим. Молярную теплоемкость при постоянном давлении определим по формуле (3) с учетом, что
), называется изобарическим. Молярную теплоемкость при постоянном давлении определим по формуле (3) с учетом, что 
 :
:
 (8)
(8)
Возьмем дифференциал от правой и левой частей уравнения (1):
 ,
,
так как  ;(
;( ), получим:
), получим:
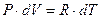 (9)
(9)
Подставив в (8) вместо 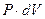 его значение из (9) и учитывая, что
его значение из (9) и учитывая, что  , получим значение молярной теплоемкости при постоянном давлении:
, получим значение молярной теплоемкости при постоянном давлении:
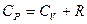 , или
, или 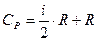 (10)
(10)
Следовательно,  на величину универсальной газовой постоянной.
на величину универсальной газовой постоянной.
3. Изотермический процесс. Изотермическим называется процесс, протекающий при постоянной температуре ( ,
, 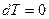 , а следовательно
, а следовательно 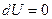 ). В этом процессе внутренняя энергия не меняется, а все подводимое тепло идет на совершение работы (
). В этом процессе внутренняя энергия не меняется, а все подводимое тепло идет на совершение работы (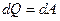 ). При изотермическом процессе при любых изменениях давления или объема:
). При изотермическом процессе при любых изменениях давления или объема:
 (11)
(11)
Молярная теплоемкость при изотермическом процессе равна бесконечности.
4. Адиабатический процесс. Процесс, протекающий без теплообмена с окружающей средой, называется адиабатическим ( ).
).
Первое начало термодинамики (2) при таком процессе имеет вид:
 ,
,
Откуда  , то есть при адиабатическом расширении или сжатии, работа совершается газом только за счет изменения внутренней энергии газа.
, то есть при адиабатическом расширении или сжатии, работа совершается газом только за счет изменения внутренней энергии газа.
Адиабатический процесс описывается уравнением Пуассона, одна из форм которого имеет вид:
 , (12)
, (12)
где 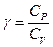 - отношение, называемое постоянной Пуассона [1].
- отношение, называемое постоянной Пуассона [1]. 
2.Принцип работы экспериментальной установки и вывод рабочих формул.
 Экспериментальная установка состоит из баллона А (рис.1), соединенного с водя-ным манометром В и с насосом. С помо-щью крана С баллон А может быть соеди-нен с атмосферой. Если насосом нака-чать в баллон некото-рое количество воз-духа, то давление и температура воздуха внутри баллона повы-сятся. Вследствие те-плообмена воздуха с окружающей средой через некоторое вре-мя температура воз-духа, находящегося в баллоне, сравняется с температурой внешней среды (температурой в аудитории)
Экспериментальная установка состоит из баллона А (рис.1), соединенного с водя-ным манометром В и с насосом. С помо-щью крана С баллон А может быть соеди-нен с атмосферой. Если насосом нака-чать в баллон некото-рое количество воз-духа, то давление и температура воздуха внутри баллона повы-сятся. Вследствие те-плообмена воздуха с окружающей средой через некоторое вре-мя температура воз-духа, находящегося в баллоне, сравняется с температурой внешней среды (температурой в аудитории)  , а давление уменьшится до
, а давление уменьшится до  , где
, где 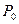 -начальное (атмосферное) давление, а
-начальное (атмосферное) давление, а  -добавочное давление, измеряемое разностью уровней водяного манометра В.
-добавочное давление, измеряемое разностью уровней водяного манометра В.
Состояние воздуха при установившемся давлении будет характеризоваться: давлением  , объемом
, объемом  (объем бал-лона), температурой
(объем бал-лона), температурой  . Состояние с такими параметрами воздуха назовем I.
. Состояние с такими параметрами воздуха назовем I.
Откроем на короткое время кран С, часть воздуха из баллона выйдет в атмосферу. Процесс выхода (расширения) воздуха протекает быстро, воздух не успевает обмениваться теплом с окружающей средой, поэтому его можно считать адиабатическим.
В конце адиабатического процесса состояние газа, (назовем его II) будет следующим: объём газа увеличится до 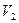 , температура понизится до
, температура понизится до  , а давление сравняется с атмосферным
, а давление сравняется с атмосферным 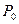 .
.
Параметры воздуха в состоянии II: давление 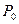 ; объём
; объём 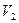 , температура
, температура  .
.
К состоянию I и II применим уравнение Пуассона (12)
 (13)
(13)
Охладившийся воздух в баллоне через некоторое время нагреется вследствие теплообмена до температуры в лаборатории  , давление возрастет до некоторой величины
, давление возрастет до некоторой величины  , а объем останется прежним
, а объем останется прежним 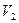 . Такое состояние воздуха назовем III.
. Такое состояние воздуха назовем III.
Параметры воздуха в III состоянии: давление  , объем
, объем 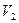 , температура
, температура  .
.
Переход воздуха из состояния II в состояние III является изохорическим нагреванием. Уравнение этого процесса имеет вид:
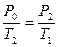 (14)
(14)
Исключив из уравнений (13) и (14) температуры, получим:
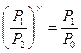 (15)
(15)
Логарифмируя уравнение (15), получим:
 .
.
Так как значения  и
и  значительно меньше значения атмосферного давления
значительно меньше значения атмосферного давления 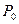 , то после разложения
, то после разложения  и
и 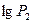 в ряд Тейлора, можно взять только два первых члена:
в ряд Тейлора, можно взять только два первых члена:
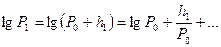 ,
,
 ,
,
тогда:
 . (16)
. (16)
Формула (16) является рабочей для нахождения постоянной Пуассона.
Из выражений (7) и (10) можно оценить число степеней свободы для воздуха (смеси нескольких газов):
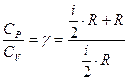 , откуда
, откуда
 (17)
(17)
Из выражения (17) следует, что  зависит только от
зависит только от  .
.






