Описание метода и установки для определения коэффициента вязкости

Лабораторная работа №8

 

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ МЕТОДОМ СТОКСА

 

Цель работы: Познакомиться со способом определения коэффициента вязкости жидкости методом Стокса.

 

Оборудование: Стеклянный цилиндр с исследуемой жидкостью, измерительная шкала с миллиметровыми делениями, микрометр, секундомер, набор металлических шариков.

1. Теоретическая часть

Явления переноса

Явлениями переноса в термодинамически неравновесных системах называются особые необратимые процессы, в результате которых происходит пространственный перенос энергии либо массы, или импульса. К явлениям переноса относятся теплопроводность (обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение (обусловлено переносом импульса).

 

Внутреннее трение (вязкость)

Механизм возникновения внутреннего трения между параллельными слоями жидкости (газа), движущимися с различными скоростями, заключается в том, что из-за хаотичного теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее - увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.

Сила внутреннего трения между двумя слоями жидкости (газа) определяется по закону Ньютона:

(1)

где - коэффициент динамической вязкости, коэффициент пропорциональности,

- градиент скорости (градиентом скорости называется изменение скорости на единицу длины в направлении, перпендикулярном скоростям v₁ и v₂ (рис.1),

 

Рис. 1

 

– площадь слоя, на который действует сила .

В системе СИ единица измерения :

Из (1) получаем: равен динамической вязкости среды, в которой при ламинарном течении и градиенте скорости с модулем, равным 1 м/с на 1м, возникает сила внутреннего трения 1 Н на 1м² поверхности касания слоев.

Исходя из основных представлений молекулярно-кинетической теории, коэффициент вязкости газов равен:

, (2)

где – плотность газа, - средняя длина свободного пробега молекул, - (3)

средняя скорость движения молекул (здесь -универсальная газовая постоянная, - термодинамическая температура, -молярная масса газа).

Из (2) и (3) следует, что коэффициент вязкости газов возрастает с увеличением температуры. Динамический коэффициент вязкости жидкостей примерно в 10⁴ раз больше, чем у газов и уменьшается с возрастанием температуры.

 

Описание метода и установки для определения коэффициента вязкости

Установка для определения коэффициента вязкости состоит из высокого цилиндрического сосуда, наполненного исследуемой жидкостью (см. рис. 2).

 

Метод Стокса основан на определении скорости медленно движущихся в жидкости тел сферической формы. Рассмотрим падение тела (в нашем случае – металлического шарика) в вязкой покоящейся жидкости. На тело действуют следующие силы:

1. Сила тяжести, направленная вертикально вниз:

, (4),

где - радиус шарика, – плотность материала шарика, - ускорение свободного падения.

2. Сила Архимеда, направленная вертикально вверх:

, (5)

где V_ш – объем шарика, – плотность жидкости,

3. Сила сопротивления (эмпирически установленная

Дж. Стоксом), направленная вертикально Рис.2 вверх:

Рис 2

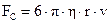, (6)

где v – скорость падения тела.

Выражение (6) справедливо при обтекании тела жидкостью (газом) без образования вихрей.

Направление сил показано на рис 2.

Рис 2

При движении тела в жидкости, ее молекулы взаимодействуют с молекулами тела. За счет действия межмолекулярных сил в процесс движения вовлекаются соседние молекулы жидкости. Появляется слой жидкости, движущийся вместе с телом со скоростью движения тела. Этот слой увлекает в своем движении соседние слои жидкости, которые на некоторый период времени приходят в плавное безвихревое движение (случай малых скоростей и малых размеров тела).

Вначале скорость движения тела будет возрастать, так как сила тяжести больше суммы сил сопротивления и силы Архимеда.

По второму закону Ньютона:

(7)

По мере увеличения скорости тела сила сопротивления будет также возрастать, наступит такой момент, когда сила тяжести уравновесится суммой сил и , т. е. можно считать, что тело падает с постоянной скоростью. Ускорение станет равным нулю и формула (7) с учетом (4), (5), (6) запишется так:

. (8)

Учитывая, что скорость тела постоянна и равна:

, (9),

где 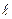– путь, пройденный в жидкости, t- время, а также, что диаметр тела , для коэффициента вязкости из (8), учитывая (9), получим:

 

(10)

Выражение (10) справедливо лишь при условии d<<D, где D – диаметр сосуда, в который помещается исследуемая жидкость. На практике также необходимо следить за тем, чтобы при движении тело не приближалось к стенкам сосуда.

 

1. Экспериментальная часть.