ИЗУЧЕНИЕ СЛОЖЕНИЯ КОЛЕБАНИЙ
Методические указания к лабораторной работе № 28 по физике
(Раздел «Электричество и магнетизм»)
Ростов-на-Дону 2013
УДК 530.1
Составители: Т.П. Жданова, В.В. Илясов, О.А.Лещева, О.М. Холодова
Изучение сложения колебаний: метод. указания к лабораторной работе № 28 по физике (Раздел «Электричество и магнетизм»). – Ростов н/Д: Издательский центр ДГТУ, 2013. – 11с.
Методические указания содержат краткое описание рабочей установки и методики определения основных характеристик при сложении колебаний.
Предназначены для студентов инженерных специальностей всех форм обучения при выполнении лабораторного практикума по физике (раздел «Электричество и магнетизм»).
Печатается по решению методической комиссии факультета
«Нанотехнологии и композиционные материалы»
Научный редактор д-р техн. наук, проф. В.С. Кунаков
© Издательский центр ДГТУ, 2013
 |
Цель работы: Познакомиться с методом сложения одинаково направленных и взаимно перпендикулярных электрических колебаний.
Приборы и принадлежности: Два генератора Г3-34 и Г3-118, осциллограф С1-72, плата с резисторами и выключателями.
Теория метода
Сложение двух одинаково направленных гармонических колебаний.
Рассмотрим сложение двух гармонических одинаково направленных колебаний с одинаковой частотой:
.
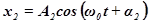Воспользуемся методом векторной диаграммы для определения вида и параметров результирующего колебания (рис.1). Каждое колебание в отдельности представляет собой вектор (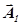
и 
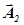), длина которого равна амплитуде колебания, а направление вектора образует с осью 
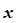угол, равный начальной фазе (
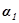и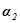 
) колебания. По правилу сложения векторов построим результирующий вектор 
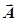. Результирующее колебание будет гармоническим колебанием с частотой 
, амплитудой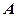 
и начальной фазой 
:
,
где 
,
.
Особый интерес представляет случай, когда два складываемых колебания одинакового направления мало отличаются по частоте. Результирующее движение при этих условиях можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такое колебание называется биением.
Пусть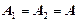 
, 
, частота одного колебания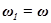 
, а частота второго колебания 
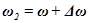, причем 
.
Тогда уравнения складываемых колебаний будут иметь следующий вид:
Уравнение результирующего колебания имеет вид:
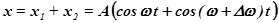
(1).
(во втором множителе пренебрегли членом 
по сравнению с 
).
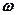График функции (1) для случая 
изображен на рис. 2.
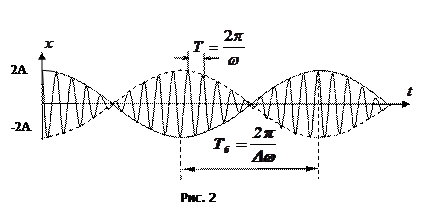
Величина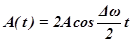 
, характеризующая размах колебаний при биениях, изменяется в пределах от 0 до 
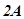с циклической частотой 
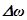. Период и частота биений соответственно равны:
;
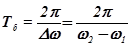. (2)
Сложение взаимно перпендикулярных колебаний
Допустим, что материальная точка (тело) может совершать колебания как вдоль оси 
, так и вдоль перпендикулярной оси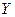 
по законам:
,
где 
- разность фаз складываемых колебани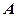й, и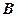 
— амплитуды колебаний.
Уравнение траектории в общем виде:
.
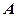Траектория – эллипс (рис.3). Ориентация в плоскости ХУ осей эллипса, а также его размеры зависят от амплитуд и 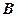складываемых колебаний и разности их начальных фаз 
.
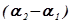Если частоты взаимно перпендикулярных колебаний неодинаковы, то траектория результирующего движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу.
Форма этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. На рис. 4 представлены фигуры Лиссажу для различных соотношений частот (указаны слева) и разностей фаз (указаны вверху).
По виду фигур можно определить неизвестную частоту по известной или определить отношение частот складываемых колебаний. Поэтому анализ фигур Лиссажу – широко используемый метод исследования соотношений частот и разности фаз складываемых колебаний, а также формы колебаний.
Рис.4
