ЛАБОРАТОРНАЯ РАБОТА № 1.12
«ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ТРЕНИЯ КАЧЕНИЯ И ТРЕНИЯ СКОЛЬЖЕНИЯ С ПОМОЩЬЮ НАКЛОНОГО МАЯТНИКА»
I. Цель работы: определение коэффициентов трения скольжения и трения качения стального шара по стальной пластине.
II. Описание установки.
Для выполнения работы используется установка ФМ-16, общий вид которой представлен на рис. 1. На основании 1, снабженном регулируемыми опорами, укреплена стойка 2, к верхней части которой на кронштейне 3 крепится наклонная платформа 4. Угол платформы к вертикали можно изменять с помощью винта 5. Значение этого угла индицируется на шкале 6 отвесом 10 с нитью 11, закрепленной на кронштейне 12. В верхней части платформы крепится наклонный маятник, состоящий из стержня 7 с обоймой 8, в которой закрепляется стальной шар. Опора 9 на верхнем конце стержня 7 позволяет ему свободно отклоняться в плоскости, параллельной платформе 4. Обойма 8 снабжена винтом для стопорения шара при измерении коэффициента трения скольжения.
III. Методика измерений и расчетные формулы.
Если маятник массой m отклонить вдоль наклонной плоскости на некоторый угол α и отпустить, то начнутся колебания, которые будут затухать под действием силы трения маятника о плоскость, сопротивления среды и трения в 
подвесе маятника. Основной причиной в данном случае будет сила трения о плоскость; две другие силы трения несущественны и ими можно пренебречь. На маятник в отклоненном положении действуют четыре силы: сила тяжести mg, сила N нормальной реакции плоскости, сила FTР трения о плоскость и сила Т натяжения подвеса. Сила трения связана с силой реакции плоскости законом Амонтона — Кулона:
, (1)
где f - коэффициент трения.
Разложим силу тяжести на компоненты mg ||, параллельную плоскости, и 
, перпендикулярную плоскости. Сила N нормальной реакции уравновешивает компоненту :
,
где γ — угол отклонения плоскости от вертикали.
Тогда для силы трения имеем:
Обозначим начальный угол отклонения маятника вдоль плоскости α0, максимальный угол в противоположную сторону (через половину периода) α1/2, угол отклонения через период α 1. При медленном убывании амплитуды потери энергии за каждый период приблизительно одинаковы и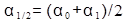 
. За период точка касания маятником плоскости проходит путь:
.
При этом сила трения совершает работу:
. (2)
На величину этой работы уменьшается полная механическая энергия маятника. В крайних положениях эта энергия представлена только потенциальной компонентой mgh, поэтому:
, (3)
где h 0 и h 1 — высоты подъема маятника в крайних положениях, соответствующие углам α0 и α1 соответственно.
Связь высоты подъема маятника с углом отклонения определим из рис. 3. В отклоненном положении центр тяжести маятника поднят вдоль плоскости на отрезок BD = AC = ℓ(1 – cosα). Из треугольника BDE получаем:
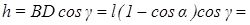
Последнее приближенное равенство справедливо при малых углах, в этом случае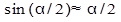 
. Подставляя выражение для каждой из высот в уравнение (3) и учитывая формулу (2), получим:
.
Сократив с обеих сторон равенства одинаковые множители и произведя преобразования, получим следующее выражение:
. (4)
Рассмотрим n последовательных колебаний наклонного маятника. Формула аналогичная (4) будет справедлива для каждого из n периодов:
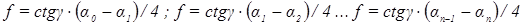. (5)
Здесь α1, α2 … αn — угловые амплитуды отклонения после второго, третьего... n -го периода колебаний. При сложении всех выражений (5) в правой части все промежуточные углы α2, α3 … αn–1 сократятся. После деления на число периодов п получим окончательную формулу для определения коэффициента трения:
. (6)
Для маятника в виде шарика, катящегося без проскальзывания по наклонной платформе, основной диссипативной силой является сила трения качения F тр.к. Тормозящий момент силы трения качения пропорционален силе нормальной реакции:
, (7)
где f 1 - коэффициент трения качения, имеющий размерность длины, R – радиус кривизны катящегося тела. Рассуждения, приведенные выше для трения скольжения, можно повторить для трения качения, используя вместо формулы (1) соотношение (7). При этом для коэффициента трения качения получим:
. (8)
IV. Порядок выполнения работы.
