Изучение законов колебательного движения с помощью физического маятника

ИЗУЧЕНИЕ ЗАКОНОВ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ ФИЗИЧЕСКОГО МАЯТНИКА

Методические указания к лабораторной работе №2

 

(Раздел «Механика»)

 

 

Ростов-на-Дону 2010

 

 

Составители: В.С. Ковалёва, О.А. Лещёва, О.М. Холодова.

 

 

УДК 530.1

 

 

ИЗУЧЕНИЕ ЗАКОНОВ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ ФИЗИЧЕСКОГО МАЯТНИКА: Метод. указания. -Ростов н/Д:

Издательский центр ДГТУ, 2010. - 12 с.

 

 

Указания содержат краткое описание рабочей установки и методики определения момента инерции физического маятника.

Методические указания предназначены для студентов инженерных специальностей всех форм обучения при выполнении лабораторных работ по физике (раздел «Механика и молекулярная физика»).

 

 

Печатается по решению методической комиссии факультета «Нанотехнологии и композиционные материалы»

 

Научный редактор проф., д.т.н. В.С.Кунаков

 

© Издательский центр ДГТУ, 2010

 

Лабораторная работа №2

 

ИЗУЧЕНИЕ ЗАКОНОВ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ ФИЗИЧЕСКОГО МАЯТНИКА

Цель работы:

Изучить колебательный процесс на примере физического маятника. Определить приведенную длину и моменты инерции физического маятника.

 

Оборудование: экспериментальная установка.

 

1. Теоретическая часть.

 

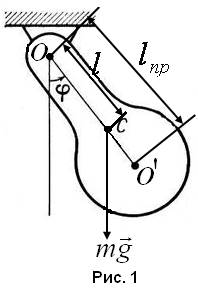Физический маятник - твердое тело, которое может совершать колебания под действием силы тяжести относительно неподвижной горизонтально расположенной оси, не проходящей через центр масс тела (рис.1). Такая ось называется осью колебания, точка 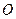– точкой подвеса маятника. Плоскость, проходящая через точк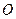и и 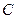перпендикулярно оси колебания, называется плоскостью колебания. В положении равновесия центр масс маятника 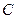находится под точкой подвеса маятника 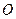, на одной вертикали.

При отклонении маятника от положения равновесия на угол 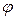возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен:

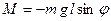, (1)

где 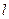- расстояние между точкой подвеса и центром масс маятника, 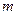– масса физического маятника.

Знак “ - ” означает, что вращательный момент имеет такое направление, что стремится вернуть маятник в положение равновесия.

На основании основного уравнения динамики вращательного движения можно написать:

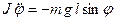, (2)

где 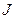– момент инерции маятника относительно оси, проходящей через точку подвеса, 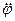- угловое ускорение маятника.

В случае малых колебаний (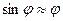), уравнение (2) можно записать:

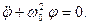(3)

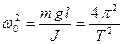где (4)

Из уравнения (3) следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания. Период колебаний можно определить из (4):

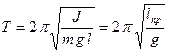(5)

где 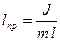(6) называется приведенной длиной физического маятника.

Приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

Центр качания - это точка на прямой, соединяющей точку подвеса с центром масс, лежащая на расстоянии приведенной длины от оси колебания (точка 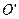на рис.1).

По теореме Штейнера момент инерции маятника равен:

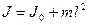, (7)

где 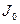- момент инерции относительно оси, параллельной оси колебания и проходящей через центр масс маятника, 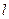- расстояние от оси вращения до центра масс.

Решая (6) и (7), получим 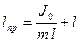. (8)

Из (8) видно, что 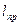всегда больше 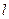, так что точка подвеса и центр качания лежат по разные стороны от центра масс.

Для определения 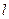поступим следующим образом. Подвесим физический маятник в точке 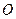. Момент инерции относительно точки 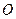, с учетом формулы (5), равен:

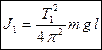, (9)

где 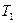- период колебаний относительно точки .

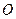Если маятник перевернуть, то момент инерции относительно точки 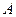равен:

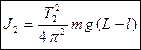, (10)

где 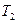- период колебаний относительно точки подвеса .

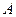Воспользовавшись формулой (7), имеем:

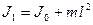(11)

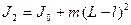(12)

Вычтем из (12) формулу (11) и получим:

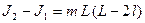(13)

Вычтем из (10) выражение (9) и получим

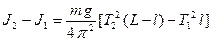(14)

Решая (13) и (14), имеем

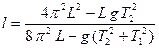(15)

Поскольку периоды колебаний находятся как

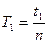и 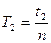, получаем рабочую формулу:

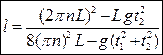. (16)

 

В работе моменты инерции маятника определяются по формулам (9) и (10) с учетом (16).

Порядок выполнения работы.

Задание. Определение приведенной длины и момента инерции физического маятника.

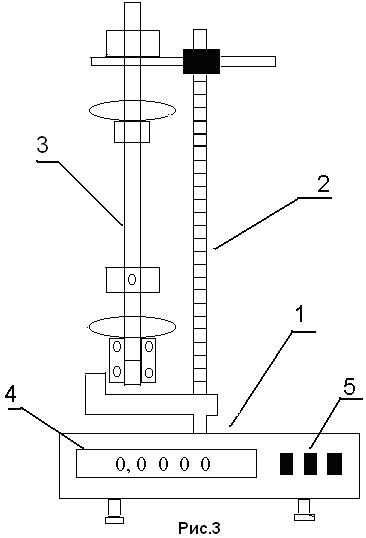
1. Основание (1) установки (рис.3) отрегулировать так, чтобы положение стойки (2) было строго вертикально.

2. Установить “ноль” в окошке секундомера (4) при помощи кнопки “сброс” (5).

3. Отвести рукой маятник в крайнее положение на небольшой угол (≈10˚). Отпустить маятник и нажать кнопку “пуск” (5).

4. Измерить время 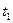для n=10-20 полных колебаний (по указанию преподавателя). В окошке (4) идет счет полным колебаниям. Кнопку “стоп” (5) следует нажать в тот момент, когда в окошке (4) высветится предпоследнее по счету колебание.

5. Измерения повторить пять раз. Результаты измерения времени и числа колебаний занести в таблицу 1.

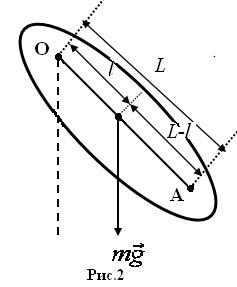
6. Перевернуть физический маятник, подвесить его в точке 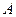(рис.2), повторить пункты 3-5 (определить время ).

 

 

 

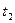7. Измерить расстояние 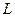между двумя точками подвеса физического маятника (рис.2) и результат занести в таблицу 1.

8. По формуле (16) рассчитать 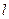, используя средние значения 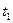и .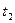

9. Рассчитать моменты инерци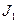и и 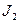по формулам (9) и (10).

10. Приведенную длину 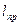рассчитать по формуле: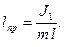

11. Провести статистическую обработку измерений времени и заполнить таблицы 2 и 3.

12. Относительные и абсолютные погрешности, по указанию преподавателя, определить по следующим формулам и занести в таблицу 4:

 

 

 

 

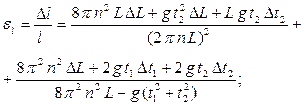
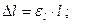
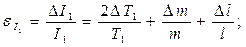
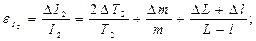
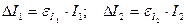
Таблица 1

 

№ n/n	n	m	t1	t2	L		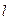l пр	J1	J2
		кг	с	c	м	м	м	кг·м2	кг·м2
Ср.зн.

 

 

Таблица2

 

№ n/n	t1	Δt1	(Δt1)2	Sn,t	tn,α	Δt1сл	Δt1пр	Δt1дов	ε1
	c	c		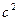c		c	c	c	%
Ср.зн.

 

 

Таблица3

 

№ n/n	t2	Δt2	(Δt2)2	Sn,t	tn,α	Δt2сл	Δt2пр	Δt2дов	ε1
	c	c		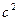c		c	c	c	%
Ср.зн.

Таблица 4

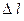
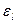
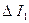
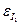
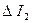
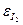
м	%		%		%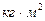

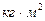
Контрольные вопросы

1. Что такое колебание? Собственное колебание? Свободное колебание? Гармоническое колебание?

2. Дайте определения амплитуды, фазы, периода, частоты и циклической частоты колебания?

3. Как можно определить период колебаний маятника экспериментально?

4. Запишите уравнение гармонического колебания, поясните физический смысл всех входящих в него величин.

5. Получите формулу для расчета максимальной скорости колеблющейся точки.

6. Получите формулу для расчета максимального ускорения колеблющейся точки.

7. Получите дифференциальное уравнение гармонических колебаний.

8. Что называется физическим маятником?

9. Выведите формулу периода колебаний физического маятника.

10. Что такое приведенная длина физического маятника?

11. Что называют центром качания физического маятника?

Рекомендуемая литература

1. Савельев И.В. Курс общей физики (т.1). М.: Наука, СПб.: Лань, 2006.

2. Трофимова Т.И. Курс физики. М.: Высш. Шк., 2004.

3. Справочное руководство по физике. Ч.1. Механика, молекулярная физика, электричество, магнетизм: Учеб.-метод. пособие.-Ростов н/Д: Издательский центр ДГТУ, 2009.

4. Колебания и волны: Учебное пособие.-Ростов н/Д: Издательский центр ДГТУ, 2009.

5. Федосеев В.Б. Физика. Ростов н/Д: Феникс, 2009.

 

Техника безопасности

 

1. К работе с установкой допускаются лица, ознакомленные с её устройством и принципом действия.

2. Для предотвращения опрокидывания установки необходимо располагать её только на горизонтальной поверхности.

 

 

Составители: В.С. Ковалёва, О.А. Лещёва, О.М. Холодова.