Лабораторная работа № 13
КРАТКАЯ ТЕОРИЯ. При движении слоёв жидкости или газа с различными скоростями между слоями действуют силы внутреннего трения или силы вязкости. Численное значение силы вязкости можно определить по формуле Ньютона:
,
где η – коэффициент внутреннего трения или коэффициент динамической вязкости; S – площадь соприкасающихся слоёв; 
– градиент скорости.
Коэффициент динамической вязкости может быть выражен формулой:
,
т. е. он численно равен силе внутреннего трения, возникающей между двумя слоями жидкости или газа, имеющими площадь соприкосновения, равную единице, при градиенте скорости, равном единице.
В системе СГС динамическая вязкость измеряется в пуазах, а в системе СИ – в Па×с.
Коэффициент динамической вязкости численно равен импульсу при упорядоченном движении, переносимому за единицу времени через единицу площади соприкасающихся слоёв при градиенте скорости, равном единице.
Наряду с коэффициентом динамической вязкости часто употребляют коэффициент кинематической вязкости, определяемый следующим образом:
,
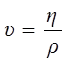где ρ – плотность жидкости или газа. Коэффициент динамической вязкости газов значительно меньше, чем жидкостей.
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Для определения коэффициента динамической вязкости воздуха воспользуемся методом истечения воздуха через капилляр. Экспериментальная установка изображена на рис. 1. Один конец капилляра К, через который протекает воздух, с помощью тройника 1 соединяется с осушительной склянкой О и левым коленом манометра М. Другой конец капилляра с помощью тройника 2 соединяется со стеклянным баллоном (10 л) и правым коленом манометра М. Осушительная склянка наполнена хлористым кальцием, поглощающем пары воды из протекающего через неё воздуха. Склянка закрыта резиновой пробкой, в которой имеется небольшое отверстие.
Если при закрытом кране С воронки открыть кран В, то вследствие вытекания воды давление в баллоне будет уменьшаться и в него будет всасываться воздух, который пройдёт через осушитель и капилляр.
Скорости движения бесконечно тонких цилиндрических слоёв воздуха, расположенных на различных расстояниях от оси капилляра, будут различны. В случае, если установившееся течение является ламинарным, скорости по сечению капилляра распределены по параболическому закону. Если считать, что для слоя, прилегающего к стенкам капилляра, имеет место явление прилипания, то скорость этого слоя равна нулю. Наибольшая скорость будет на осевой линии капилляра. Вследствие различия скоростей слоёв между ними возникнут силы внутреннего трения. При установившемся движении сила вязкости, действующая на цилиндрический объём и приложенная к боковой поверхности цилиндра, уравновешивает разность сил давления, действующих на основания цилиндра.
На концах капилляра при протекании через него воздуха будет существовать разность давлений (давление на входе будет больше давления на выходе). При установившемся движении воздуха разность давлений будет неизменной, т. к. в этом случае параметры, характеризующие течение (скорость, давление в различных точках потока), не меняются с течением времени и являются функцией только координат.
Для случая установившегося ламинарного течения вязкой, но несжимаемой жидкости по капилляру радиусом r справедлива формула Гагена–Пуазейля:
, (1)
где V – объём жидкости, протекающий через сечение капилляра за единицу времени; (p1 - p2) – разность давлений в начале и в конце капилляра; l – длина капилляра.
Так как в отличие от жидкостей, практически несжимаемых, закон Гагена – Пуазейля в такой форме записи, строго говоря, не применим к газам. Лишь при малых разностях давлений, когда (p1 - p2)<< p 2 (и соответственно малых скоростях течения газов), сжимаемостью газов можно пренебречь и применить к ним формулу Гагена–Пуазейля.
При больших перепадах давления вследствие значительной сжимаемости газов разность давлений, приходящаяся на единицу длины капилляра, не будет постоянной, т. е. вдоль оси капилляра будет меняться градиент давления. Поэтому в этих условиях формулу (1) можно применить только к бесконечно малому участку длины капилляра.
В данной работе изменения производятся при небольших разностях давлений на концах капилляра. Поэтому для расчётов может быть использована формула (1). Объём воздуха, протекающего через сечение капилляра за время τ, будет равен:
(2)
Отсюда:
(3)
Зная значения r, p1 - p2, τ, V и l, можно определить коэффициент динамической вязкости воздуха.
При точных расчётах коэффициента динамической вязкости необходимо ввести поправку на скольжение молекул газа по внутренней поверхности капилляра (при течении газа нельзя говорить о прилипании к стенкам капилляра слоя газа, прилежащего к ним). В данной работе этими поправками можно пренебречь.
ИЗМЕРЕНИЯ. Открыв кран С воронки баллона, при закрытом кране В наполняют баллон водой на 2/3 объёма, после чего кран С перекрывают. Осторожно вынимают капилляр К, и, положив на имеющуюся стойку, определяют с помощью измерительного микроскопа его диаметр. Измерив диаметр и длину капилляра, укрепляют его в рабочем положении.
Открывают кран В и регулируют скорость истечения воды таким образом, чтобы разность уровней спирта в коленах манометра не превышала 2–2,5 см.
Убедившись в том, что течение воздуха через капилляр установилось (в этом случае h остаётся неизменным), измеряют h и с помощью секундомера определяют время τ, за которое из баллона вытекает в мензурку V = 500 см3 воды (этот объём занимает воздух).
При той же разности уровней измеряют ещё два раза время, за которое из баллона вытекает вода объёмом V = 500 см3. Вычисляют разность давлений
,
где ρ1 =0,79×103 кг/м3 (плотность спирта), и среднее значение времени из трёх измерений. Затем по формуле (3) рассчитывают вязкость воздуха.
Для того чтобы установить, было ли течение воздуха ламинарным, вычисляют число Рейнольдса по формуле:
,
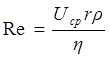где Uср - средняя скорость течения воздуха через капилляр; r – радиус капилляра; ρ – плотность воздуха при комнатной температуре и атмосферном давлении. Средняя скорость:
,
где S - сечение капилляра (S=πr2).
Плотность воздуха рассчитывают, пользуясь уравнением Клапейрона-Менделеева, взяв из таблиц её значение при нормальных условиях. Если Rе < 1000, то течение ламинарно.
ЗАМЕЧАНИЕ.
Если время вытекания одного и того же объёма воды определяется при нескольких отличающихся разностях давлений, то усреднять это время нельзя. В этом случае коэффициент динамической вязкости рассчитывается три раза, а затем находится его среднее значение.
ЗАДАНИЕ.
1. Пользуясь описанной выше методикой, определите коэффициент динамической вязкости воздуха η при комнатной температуре. Определите с помощь термометра комнатную температуру.
2. Определите с помощью барометра атмосферное давление. Рассчитайте плотность воздуха при комнатной температуре и атмосферном давлении. Зная η и ρ, определите коэффициент кинематической вязкости воздуха при комнатной температуре.
3. Рассчитайте предельные, относительную и абсолютную погрешности измерения коэффициента динамической вязкости.
