Лабораторная работа № 2
КРАТКАЯ ТЕОРИЯ. Теплоемкость тела - физическая величина, показывающая количество теплоты, которое необходимо сообщить телу в данном термодинамическом процессе, для изменения его температуры на один кельвин:
.
Молярной теплоемкостью тела называется физическая величина, показывающая количество теплоты, необходимое для изменения температуры вещества в количестве одного моля на один кельвин:
,
где M - количество вещества.
Удельной теплоемкостью тела называется физическая величина, показывающая количество теплоты, необходимое для изменения температуры тела массой 1 кг на один кельвин:
.
Теплоемкость газов зависит от условий, при которых производится изменение их температуры. В зависимости от процесса изменения состояния газа теплоемкость бывает:
1. Изобарный процесс: теплоемкость при постоянном давлении 
.
2. Изохорный процесс: теплоемкость при постоянном объеме 
.
3. Изотермический процесс: теплоемкость бесконечно большая.
4. Адиабатный процесс: теплоемкость равна нулю.
Молярные теплоемкости идеальных газов связаны уравнением, носящим имя Р. Майера:
,
где R – газовая постоянная.
Адиабатным называется процесс, протекающий в системе без теплообмена с окружающей средой. К ним близки все быстро протекающие процессы. Например, адиабатным можно считать процесс распространения в упругой среде звуковых (ультразвуковых) волн.
Адиабатные процессы описываются уравнением Пуассона:
,
где g - показатель Пуассона. Показателем Пуассона называется отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме:
.
Определение величины показателя Пуассона можно производить различными методами (в частности, акустическими). В данной работе предлагается использовать для определения величины 
воздуха метод его адиабатного расширения.
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Установка для измерения воздуха (рис. 1) состоит из стеклянного баллона большой емкости, который при помощи крана может соединяться с насосом или атмосферой. Разность между давлением воздуха в баллоне и атмосферным давлением измеряется открытым жидкостным манометром, одно из колен которого соединяется с сосудом.
Эксперимент проходит в три этапа:
1. Сжатие воздуха в баллоне. Соединив при помощи крана и резинового шланга баллон с насосом, в него нагнетают воздух. Когда разность уровней в манометре становится равной 15-20 см, кран поворачивают до такого положения, при котором воздух в баллоне будет отсоединен как от насоса, так и от окружающей среды. Процесс нагнетания воздуха в баллон происходит довольно быстро и близок к адиабатному. Поэтому температура воздуха в баллоне увеличивается. Для установления равновесного состояния требуется некоторое время (2-3 минуты), в течение которого происходит теплообмен воздуха в баллоне с окружающей средой. При этом уровни в манометре будут перемещаться. Когда температура воздуха в баллоне T1 станет равной комнатной, перемещение уровней в манометре прекратится. Измерив в данном состоянии разность уровней в манометре 
, соответствующее давление 
определяют в виде:
,
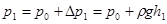где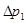 
- разность давлений, соответствующая первому состоянию газа в баллоне,
r - плотность манометрической жидкости.
2. Адиабатное расширение. Поворотом крана соединяют воздух, находящийся в баллоне, с атмосферой. Кран закрывают, как только давление в баллоне станет равным атмосферному, о чем судят по показаниям манометра (h =0).
Так как процесс расширения происходит быстро, теплообменом между содержимым баллона и окружающим воздухом можно пренебречь, то есть наблюдается адиабатное расширение воздуха в баллоне, сопровождающееся понижением температуры до T2 при давлении 
.
Согласно уравнению Пуассона при адиабатном расширении начальное и конечное состояния газа связаны соотношением:
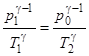. (1)
3. Изохорное нагревание. После возвращения крана в прежнее положение воздух в баллоне начинает нагреваться вследствие теплообмена с окружающей средой, давление его увеличивается, о чем можно судить по перемещению уровней в манометре. Когда температура воздуха в баллоне станет равной комнатной температуре 
, перемещение уровней прекратится, их разность h 2станет постоянной. Давление в баллоне в данном состоянии определяется в виде:
.
Применим закон Гей-Люссака:
. (2)
Исключив из уравнений (1) и (2) температуры Т1 и Т2, получим:
. (3)
Логарифмируя уравнение (3), преобразуем его:
. (4)
Учитывая, что 
и 
, а 
при 
, найдем:
И.
Тогда формула (4) примет вид:
, (5)
Искомое отношение
. (6)
Следовательно, для определения показателя Пуассона воздуха достаточно измерить h1 и h2 в конце 1 и 3 этапов измерений.
ЗАДАНИЕ
1. Ознакомиться с устройством крана, определив положения, в которых он соединяет баллон с насосом, атмосферой, а так же когда он закрыт.
2. Открыть кран и накачать воздух в баллон так, чтобы разность уровней жидкости в манометре составляла 20-25 см. Закрыть кран и, выждав 2-3 минуты (до тех пор, пока уровни жидкости в трубах манометра перестанут изменяться), отсчитать по шкале уровни левой и правой трубки манометра.
3. Быстро открыть и тотчас закрыть кран. Снова выждав 2-3 минуты, отсчитать положение жидкости в трубах манометра.
4. Опыт повторить 8 раз, изменяя начальное давление воздуха в баллоне. Результаты каждого измерения занести в таблицу.
5. Рассчитать среднее значение показателя Пуассона воздуха, вычислить абсолютную погрешность каждого измерения и среднюю абсолютную погрешность.
Результат представить в виде: 
.
