1. Функція у = f(х), визначена на множині Х, називається обмеженою на цій множині, якщо існує таке число М > 0, що для усіх х 
Х виконується нерівність
| f (х) | ≤ M. Звідси витікає, що графік обмеженої функції розташований між прямими у = М і у = - М.
2. Нехай функція у = f(х), визначена на множині Х, тоді якщо для будь-яких двох значень х1, х2 Х аргументів з нерівності х1< х2 слідує нерівність:
1) f(х1) < f(х2), те функція називається зростаючою на множині Х
(більшому значенню аргументу відповідає більше значення функції);
2) f(х1) > f(х2), те функція називається спадаючою на множині Х
(більшому значенню аргументу відповідає менше значення функції);
3) f(х1) ≤ f(х2), те функція називається не спадаючою на множині Х;
4) f(х1) ≥ f(х2), то функція називається не зростаючою на множині Х.
Зростаючі, не зростаючі, спадаючі і не спадаючі функції на множині Х називаються монотонними на цій множині.
3. Нехай функція у = f(х), визначена на множині Х, тоді якщо для будь-якого х Х виконується умова:
1) f(-х) = f(х), то функція називається парною.
2) f(-х) = - f(х), то функція називається непарною.
Графік парної функції симетричний координатній осі Оу, а непарної - відносно початку координат О.
Наприклад, y = x2, y = cos x, y = ln |x| - парні функції, y = sin x, y = x3 - непарні функції.
Якщо функція не є парною або непарною, то вона називається функцією загального вигляду. Наприклад, y = x - 2, y =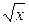 
- функції загального вигляду.
4. Функція у = f(х), визначена на множині Х, називається періодичною на цій множині, якщо існує таке число Т > 0, що для усіх х Х виконуються умови (х + Т) Х і f (х + Т) = f (х). При цьому число Т називається періодом функції. Наприклад, функції y = sin x, y = cos x - періодичні з періодом Т = 2π.
Обернена функція
Нехай задана функція у = f(х) з областю визначення Х і множиною значень Y. Якщо кожному значенню y Y відповідає одно і тільки одно значення х Х, те має місце функціональна залежність x = φ (y) з областю визначення Y і безліччю значень Х. Така функція φ(y) називається оберненою до функції f(х). Таким чином, функції у=f(х) і x = φ (y) є взаємно оберненими. Щоб знайти функцію x = φ (y), зворотну до функції у = f(х) необхідно розв‘язати рівняння f (х) = у відносно х.
Приклади: 1. Для функції 
оберненою функцією буде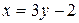 
;
2. Для функції,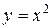 
заданої на відрізку [- 1, 1], оберненої функції не існує, тоді як для цієї ж функції заданої на відрізку [0, 1] оберненою функцією є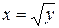 
З визначення оберненої функції виходить, що функція у = f(х) має зворотну у тому випадку, якщо функція f(х) задає взаємно однозначне відображення між областями Х і Y. Очевидно, що будь-яка монотонно зростаюча (монотонно спадаюча) функція має обернену. Помітимо, що графіки взаємно обернених функцій у = f(х) і у = φ(х) симетричні відносно бісектриси першої і третій чверті координатної площини.
Складна функція
Нехай функція z = φ (х) з множиною значень Z, визначена на множині Х і на множині Z також визначена функція у = f(z) з множиною значень Y, тоді функція у = f[φ (х)] називається складною функцією від аргументу х, а змінна z називається проміжною змінною складної функції.
Наприклад,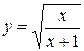 
складна функція, визначена на множині (-∞, 0) 
(-1, +∞), оскільки у = f (z) =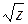 
, z = φ (х) = 
.
