Метод замены наименее значащего бита

Метод замены наименее значащего бита (НЗБ, LSB — Least Significant Bit) наиболее распространен среди методов замены в пространственной области [3, 5, 9, 14,19,20].

Младший значащий бит изображения несет в себе меньше всего информации. Известно, что человек в большинстве случаев не способен заметить изменений в этом бите. Фактически, НЗБ— это шум, поэтому его можно использовать для встраивания информации путем замены менее значащих битов пикселей изображения битами секретного сообщения. При этом, для изображения в градациях серою (каждый пиксель изображения кодируется одним байтом) объем встроенных данных может составлять 1/8 от общего объема контейнера. Например, в изображение размером 512x512 можно встроить ~32 кБайт информации. Если же модифицировать два младших бита (что также практически незаметно), то данную пропускную способность можно увеличить еще вдвое.

Популярность данного метода обусловлена его простотой и тем, что он позволяет скрывать в относительно небольших файлах достаточно большие объемы информации (пропускная способность создаваемого скрытого канала связи составляет при этом от 12,5 до 30%). Метод зачастую работает с растровыми изображениями, представленными в формате без компрессии (например, GIF и BMP) [3][2].

Метод НЗБ имеет низкую стеганографическую стойкость к атакам пассивного и активного нарушителей. Основной его недостаток— высокая чувствительность к малейшим искажениям контейнера. Для ослабления этой чувствительности часто дополнительно применяют помехоустойчивое кодирование

Перед импортом изображения-контейнера в документ MathCAD его необходимо подготовить в соответствующем редакторе и записать в виде файла в текущий (для формируемого документа MathCAD) каталог (Следует отметить, что во избежание возможных проблем с поддержкой кириллицы желательно, чтобы адрес размещения файла на диске, как, собственно, и имя файла, состояли из латинских символов). MathCAD поддерживает форматы BMP, JPEG, GIF, PCX и TGA. Как было указано выше, форматы BMP и GIF, позволяют сохранять изображения практически без потери их качества и потому более пригодны в роли носителей информации.

Рассмотрим структуру BMP-файла; он содержит точечное (растровое) изображение и состоит из трех основных разделов: заголовка файла, заголовка растра и растровых данных.

Заголовок файла содержит информацию о файле (его тип, объем и т.п.) В заголовок растра вынесена информация о ширине и высоте изображения, количество битов на пиксель, размер растра, глубина цвета, коэффициент компрессии и т.д.

Нас в первую очередь будут интересовать растровые данные — информация о цвете каждого пикселя изображения. Цвет пикселя определяется объединением трех основных цветовых составляющих красной, зеленой и синей (сокращенно, RGB). Каждой из них соответствует свое значение интенсивности, которое может изменяться от 0 до 255. Следовательно, за каждый из цветовых каналов отвечает 8 битов (1 байт), а глубина цвета изображения в целом — 24 бита (3 байта).

Шаг1

Импорт графического файла выполняется операцией Picture из позиции Insert главного меню программы. В модуле, который при этом появился, необходимо заполнить шаблон данных в левом нижнем углу, для чего в двойных кавычках следует ввести имя файла (или же, при необходимости, — полный путь его размещения на диске) и нажать клавишу <Enter>.

Рис. 5.2. Изображение-контейнер

Пример цветного изображения, восстановленного с помощью операции Picture представлен на рис. 5.3. Это изображение имеет размер 128x128 пикселей, глубина цвета 24 бита. Для возможности обработки изображения необходимо перевести цветовые характеристики каждого его пикселя в числовую матрицу. Для выполнения этой операции применяется функция READRGB ("имя файла"), возвращающая массив из трех под массивов, которые, в свою очередь, несут информацию о разложении цветного изображения на цветовые компоненты R, G и В:

С:= READRGB(”C bmp").

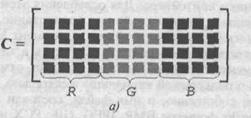
При этом три цветовых компонента размещаются один за другим в общем массиве С (рис. 5.4, а) На рис 5.4, б представлена графическая интерпретация массива С в виде изображения с градациями серого. Образ слева характеризует интенсивность красного в каждом пикселе изображения С bmp, средний — интенсивность зеленого, а тот, который справа, — интенсивность синего.

Для выделения цветовых составляющих можно использовать встроенные функции выделения соответствующих цветовых компонентов, каждая из которых возвращает массив, соответствующий определенному цветовому компоненту графического файла:

При этом три цветовых компонента размещаются один за другим в общем массиве С (рис. 5.4, а) На рис 5.4, 6 представлена графическая интерпретация массива С в виде

Рис. 6.4. Графическая интерпретация массива цветовых компонентов контейнера-оригинала

изображения с градациями серого. Образ слева характеризует интенсивность красного в каждом пикселе изображения С.bmp, средний — интенсивность зеленого, а тот, который справа, — интенсивность синего.

R:= READ_RED ("C bmp"); G:= READ_GREEN ("C bmp"), В:= READ_BLUE ("C bmp")

Шаг 2

В качестве сообщения, которое необходимо скрыть, используем, например, первые восемь абзацев из вступления данной книги. Текст сообщения сохраним в файле М txt каталога, текущего для формируемого документа MathCAD, в следующем формате:

• тип файла — обычный текст (*.txt);

• кодирование — кириллица (Windows)

Импорт текстового сообщения можно выполнить с помощью функции 11ЕАОВ1г4("имя_файла", 'тип_формата_данных"). В этом случае данные представлены как 8-битное беззнаковое целое число (байт):

М:= READBIN ("M.txt, "byte").

Результат вычисления данного выражения — матрица-столбец (вектор), каждый элемент которой соответствует расширенному ASCII-коду соответствующего символа (буквы) импортируемого сообщения. В десятичном виде коды символов могут принимать значения от 0 до 255; в двоичном виде для этого достаточно использовать 8 битов на один символ — так называемое однобайтовое кодирование, на что указывает параметр byte как аргумент функции READBIN (см. приложения В и Е).

Фрагмент импортированного сообщения, а именно коды первых 16 символов (включая пробелы) в десятичном и двоичном видах, представлен на рис. 5.5[3]

Необходимо отметить, что по умолчанию нижняя граница индексации массивов равна 0. В примерах данной книги индексация начинается с 1 (если не будет оговорено другое), что, в частности, можно установить с помощью оператора ORIGIN:= 1 в начале документа или ввести 1 в поле Array Origin на вкладке Built-in Variables диалогового окна Worksheet Options, которое вызывается из меню Tools системы MathCAD.

Проверку импортирования файла сообщения (если в качестве сообщения используется обыкновенный текст) можно выполнить с помощью вызова функции vec2str(M). Эта функция возвращает строку символов, соответствующих вектору М ASCII-кодов.[4]

Шаг 3

Перед скрытием текстового файла M.txt в контейнере C.bmp его можно защитить криптографическим кодированием. Для наглядности и краткости изложения используем модифицированный код Виженера. Вообще, для устойчивости стеганосообщения к возможным искажениям рекомендуется применять код с исправлением ошибок.

Алфавит источника сообщения зададим в виде ASCII-кодов: i: =1..256; A_i =i-1 (для большей защищенности, элементы вектора А можно переставить по определенному закону, что соответствующим образом необходимо учитывать при расшифровывании).


		11001000b
		11101101b
		11110100b
		11101110b
		11110000b
		11101100b
		11100000b
М-	М=	11110110b
		11101000b
		11111111b
		100000b
		11111111b
		11100010b
		11101011b
		11111111b
		11100101b

Рис. 6.5. Фрагмент сообщения, подлежащего скрытию

Объем алфавита источника: Na:=rows(A), где rows(A) — функция, которая возвращает количество строк массива А. В данном случае: Na - 256 символов.

Из символов алфавита задаем секретный ключ, например: К: ="@J|eKc-1980". Количество символов в ключе (по соответствующей функции): Nk:= strlen(K), Nk = 11 символов.

Объем сообщения, которое подлежит кодированию: Nm:=rows(M), Nm = 5390 символов (включая скрытые служебные ASCII-символы переноса строки и возврата каретки — см. приложение Е).

Расширяем ключ на длину сообщения (Nm), используя программный модуль (M.1).

В данном модуле функция str2vec(K) преобразует строку символов К в вектор их ASCII-кодов. Программный оператор for организовывает цикл изменения i (переменная цикла) с заданным количеством повторов (в данном случае — от 1 до Nm). Функция mod(i,Nk) возвращает остаток от деления i на Nk.

Выполняем кодирование сообщения, используя модуль (М.2)

Шаг 4

Для того чтобы при распаковке контейнера из полученного множества символов можно было четко определить начало и конец именно скрытого сообщения, целесообразно ввести соответствующие секретные метки, которые ограничивали бы это полезное содержание.

Метки должны состоять из достаточного количества символов, чтобы не принимать за метки символы случайного образования. Кроме того, для уменьшения вероятности обнаружения меток при проведении стеганоанализа желательно, чтобы коды этих символов были достаточно разнесены на ASCII-оси (например, использовать наряду с латинскими символами символы кириллицы и служебных символов — так называемая транслитерация; использование псевдослучайных последовательностей кодов символов и т.п.). Пусть метки имеют следующий вид:

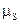=”n0ч@m0k” 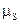=”KIHeu,6”

Ограничивающие метки добавляем в текст закодированного сообщения, для чего используем функцию stack(A,B,...), которая позволяет объединять записанные через запятую массивы. Объединение происходит путем "насаживания" матрицы А на матрицу В; полученной таким образом матрицы — на следующую матрицу (если такая присутствует) и т.д.

Понятно, что начальные матрицы должны иметь одинаковое количество столбцов, поэтому необходимо преобразовать метки из строк в векторы ASCII-кодов. Следовательно, sMe:stack {str2vec(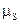), M_cod, str2vec()).

Общее количество символов в скрытом сообщении: rows(sMe)=5404. Количество НЗБ контейнера,- которое для этого необходимо (8 бит/символ): 8rows(sMe) = 43232 бита. Общее количество НЗБ контейнера: rows(C)cols(C) = 3 128 128 = 49152 > 43232 бит. Таким образом, файл изображения имеет достаточный объем для того, чтобы скрыть сообщение.

Шаг 5

Для дальнейших вычислений потребуется преобразование десятичного числа (которым по умолчанию кодируется каждый символ) в формат двоичного. Также понадобится и обратное преобразование. Поскольку данные функции в MathCAD отсутствуют (существует; как это было показано выше, только возможность преобразования формата ответа, что для наших целей неприемлемо), предлагается использовать следующие модули, смысл которых совершенно очевиден.

Преобразование двоичного числа х, которое задано матрицей-столбцом (причем первый элемент матрицы — самый младший разряд числа), в десятичное выполняется с помощью модуля (М.З).

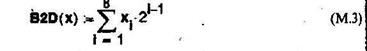
Преобразование десятичного числа в двоичное реализуется модулем (М.4)

Функция mod(x,2) возвращает остаток от деления х на 2 (0, если х четное, и 1, если х нечетное). Функция floor() возвращает наибольшее целое число, которое меньше или равняется действительному значению аргумента.

Шаг 6

Для большего удобства и наглядности дальнейших действий, развернем матрицу С в вектор, временно изменив порядок цветовых матриц с R-G-B на B-G-R, что увеличит защищенность скрытой информации (на данном этапе можно использовать более надежные, но и более сложные, алгоритмы). В нашем случае применим модуль (М.5), в, котором функция augtment(A,B,...) объединяет матрицы А, В,..., имеющие одинаковое количество строк (объединение выполняется столбец к столбцу, матрицы должны иметь одинаковое количество строк).

Операция 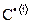позволяет выбирать i-й столбец из матрицы С', каждый из которых впоследствии прибавляется к результирующему вектору Cv. Функция cols(C') возвращает общее количество столбцов массива С.

Шаг 7

На основе вектора Cv формируем новый вектор, который уже будет содержать скрытое закодированное сообщение (модуль (М.6)).

Каждый символ закодированного сообщения (операция цикла for 1..rows(sMe)) переводится в двоичный формат (переменная b), каждый из восьми разрядов которого записывается вместо НЭБ числа, соответствующего интенсивности того или иного цвета пикселя (последнее также предварительно переводится в двоичный формат (переменная Р)).

После изменения модифицированное двоичное число Р переводится в формат десятичного и записывается в соответствующую позицию вектора Sv.

После обработки последнего символа сообщения sMe выполняется модификация элементов массива Cv, которые еще не претерпели изменений. Младшим битам каждого из таких элементов присваивается значение 0 или 1 (в данном случае — по равномерному закону распределения; функция round() возвращает округленное до ближайшего целого значение аргумента), хотя более правильно было бы провести исследование закона распределения значений уже модифицированных младших битов и соответствующим образом изменять те, которые остались (данная процедура является темой отдельного исследования и в рамках данной книги не рассматривается). Это делает невозможным со временем обнаружить факт модификации изображения.

В противном случае, проанализировав изображение, построенное из одних только НЗБ контейнера, нарушитель в большинстве случаев (если символов сообщения "не хватило" на весь контейнер) обнаружит границу ввода данных и при определенных усилиях сможет добыть скрытую информацию. Обычно, эту информацию еще необходимо расшифровать, но факт ее наличия уже будет раскрыт и вопрос защиты вернется к криптографической устойчивости используемого кодирования.

На рис. 5.6 в качестве примера представлены графические интерпретации массивов цветовых компонентов, воспроизведенные только на основе НЗБ (0/1) контейнера-оригинала (а), контейнера-результата без модификации (б) и с модификацией (в) избыточных битов. Как видим, при отсутствии "дописывания" при неполном заполнении контейнера четко прослеживается граница ввода сообщения (рис. 5.6, б) — следует напомнить, что. подмассивы R и В поменялись местами, поэтому последней модифицировалась матрица R, которая, в конце концов, и оказалась заполненной не до конца. "Дописывание" равновероятными 0 и 1 несколько исправляет ситуацию, хотя при дополнительном стеганоанализе на закон распределения значений НЗБ несоответствие сразу будет обнаружено, что еще раз подтверждает необходимость предварительного анализа распределения значений уже модифицированных битов или же хотя бы продублировать часть сообщения для заполнения всего контейнера. Также очевидно отличие между рисунками а и б.

Таким образом, желательно, чтобы изображение, которое планируется использовать в качестве контейнера, было уникальным. Тут следует заметить, что вое графические контейнеры условно разделяются на "чистые" и "зашумленные" [95].

У первых прослеживается связь между младшими и остальными семью битами цветовых компонентов, а также зависимость между самыми младшими битами.

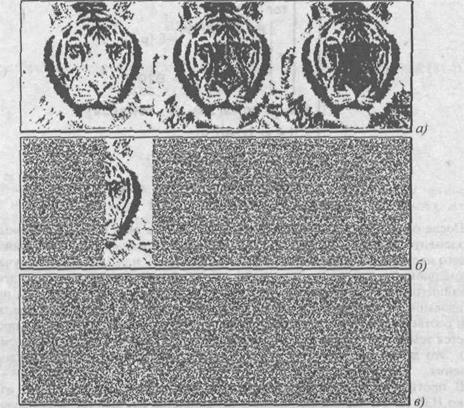
Рис. 5.6. Массивы цветовых компонентов, воспроизведенных по НЗБ

Встраивание сообщения в "чистое" изображение разрушает существующие зависимости, что, как было показано выше, легко обнаруживается. Если же изображение изначально зашумлено (сканированное изображение, цифровое фото и т.д.), то определить постороннее вложение становится на порядок сложнее, хотя и возможно при использовании теории вероятностей и математической статистики.

Также можно отметить, что для большей скрытности биты сообщения следует вносить не последовательно, а только в каждый второй или даже третий пиксель, или же подчинить внесение определенному, известному только авторизованным лицам, закону. Данные модификации легко осуществить путем внесения соответствующих незначительных изменений в модуль (М.6).

Шаг 8

Полученный с помощью модуля (М.6) вектор Sv сворачиваем в матрицу S, имеющую размерность первичной матрицы С (модули (М.7) и (М.8)).

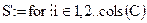(M.7)

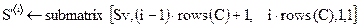
Функция submatrix(A,x,X,у,Y) возвращает часть матрицы А, которая состоит из элементов, общих для строк от х до X и столбцов от у до Y включительно.

Шаг 9

Пользуясь этой же функцией, выделяем из массива S' цветовые матрицы и расставляем их на свои места , получая контейнер-результат S (М.8).

На рис. 5.7 показана графическая интерпретация массива S в виде изображения с градациями серого и воспроизведенное по цветовым составляющим изображение-контейнер со скрытым сообщением.

Сравнивая рис. 5.7 с рис. 5.4, можно сделать вывод об отсутствии заметных визуальных отклонений.

Рис. 6.7. Контейнер-результат и его интерпретация в виде массива цветовых компонентов

Остается только записать массив 3 в файл: WRITERGB ("S_LSB.bmp"):= S. Совершенно очевидно, что объем полученного файла будет соответствовать объему файла изображения-оригинала.

Шаг 10

Дня исследования влияния на степень скрытости того, в какой из разрядов числа, характеризующего то или иное свойство пикселя (в нашем случае — интенсивность определенного цвета), будет заноситься секретная информация, в модуле (М.6) в отмеченных звездочкой строках следует вместо индекса "1" ввести индекс, соответствующий модифицируемому разряду. На рис. 5.8 изображен результат, полученный при внесении данных в 8-й (самый старший) бит числа, соответствующего интенсивности цветов.

Установлено, что визуально незаметно, если в качестве "носителей" использовать не только самый младший, но и следующий за ним бит каждого из указанных выше чисел (особенно если в изображения отсутствуют большие однотонные участки). Следовательно, в качестве одной из возможных степеней защиты возможно использование изменяемой по определенному закону поочередной записи в эти два бита. Или же, жертвуя скрытностью, можно вдвое увеличить емкость контейнера.

Рис. 5.8. Цветное изображение и массив цветовых составляющих в случае внесения скрываемых данных в 8-й бит интенсивности цветов

Шаг 11

Рассмотрим процесс распаковки скрытого сообщения. Изначально зная, что сообщение было помещено в массив цветовых компонентов, выделяем соответствующие каждому цвету подмассивы, переводя значения цветовых характеристик каждого пикселя изображения, содержащего в себе скрытое закодированное сообщение, в числовые матрицы:[5]

R*:= READ_RED ("S_LSB.bmp"); G*:= READ_GREEN (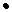); В*:= READ_BLUE ().

Из полученных матриц, соответствующим образом изменяя их порядок, аналогично (М.5), формируем вектор Sv* (модуль (М.9)).

Надлежащим образом обрабатывая каждые восемь элементов полученного век-гора, распаковываем скрытое сообщение, используя модуль (М. 10).

Следует отметить, что, поскольку заранее неизвестно, какую часть вектора Sv* займет именно полезная информация, во внимание берутся все его элементы. Значения каждого элемента формируемого при этом вектора Мf* представляет собой коды символов "квазисообщения", которые вычисляются в обратном к (М.6) порядке: каждый младший разряд восьмерки преобразованных в двоичный формат элементов вектора Sv* формирует двоичное число кода символа, формат которого далее преобразуется в десятичный. Полученное число присваивается ц-му элементу вектора Мf*.

Шаг 12

В связи с невозможностью обработки строковыми функциями 12-й версии MathCAD символов, ASCII-коды которых имеют значения от 0 до 31 включительно (за исключением служебных символов LF (код 10) и CR (код 13)), дополнительно вносится замена значений 0, 1,2,..., 31 элементов вектора Мf* соответствующим прибавлением к каждому из них коэффициента 32,5 (коэффициент является дробью для того, чтобы в дальнейшем было возможно отличить "настоящие" значения элементов массива от тех, которые перед этим имели неформатные значения). Такую замену, конечно, необходимо соответствующим образом учитывать в дальнейшем — для этого запомним номера строк вектора Мf*, элементы которых имеют дробные значения (модуль (МЛ 1)).

При этом, в первый столбец формируемого массива N заносятся номера элементов, значения которых равны 32,5 (бывшие нули), во второй столбец — номера элементов со значением 33,5 (бывшие единицы) и т.д.

Шаг 13

Зная, что текст полезной информации ограничен метками 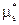:="n0ч@m0к"; := "KiHeu,6", выделяем его из извлеченного квазисообщения, используя модуль (М.12).

Вектор ASCII-кодов Мf*, предварительно преобразованный с помощью функции vec2str() в соответствующую ему строку символов, последовательно просматривается в поиске стартовой и конечной меток. Такая операция выполняется путем сравнения выделенной части строки данных с соответствующими метками, которые должны быть известны получателю.

Выделение выполняется с помощью функции substr(Мf*, ц, Р), которая возвращает подстроку длиной в 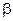символов из строки Мf*, начиная с символа (следует отметить, что в данном случае первый символ строки имеет номер, соответствующий значению встроенной переменной ORIGIN) [6]. В нашем случае, поскольку каждая из меток состоит из 7 символов, .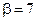

Последовательным увеличением , происходит продвижение вдоль строки данных Мf*. При выполнении указанных в модуле условий (оператор if), коэффициентам не присваиваются соответствующие значения номеров начальной и конечной позиции полезной информации в строке данных Мf*. Такие дополнительные условия, как s=0; е=0; s 0; в 0 введены для ускорения поиска.

Обратное преобразование строки символов Мf* в вектор их ASCII-кодов позволяет в этом же модуле непосредственно выделить скрытую информацию и восстановить элементы, значения которых были принудительно изменены на дробные.

Шаг 14

Распакованное сообщение требуется декодировать. Необходимые начальные условия состоят в том, что авторизованной стороне известны:

• алфавит источника сообщения (i:=1..256; A* _i:= i —1) объемом Na*:=row»{A*), Na* =256 символов;

• секретный ключ К*:= "@J|eKc-I980"с Nk*:= strlen(K*), Nk* = 11 символов;

• объем сообщения, подлежащего декодированию: Nm*:=rows(M_cod*), Nm* = 5390 символов.

С помощью модуля (М.13) секретный ключ К* расширяется на длину Nm* сообщения M_cod* (аналогично тому, как это было при кодировании сообщения — (М. 1)).

Декодирование секретного сообщения выполняется с помощью модуля (М.14).

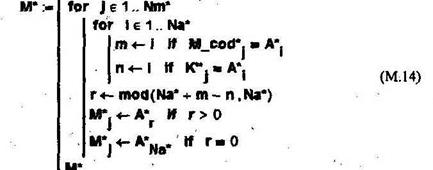
Декодированное сообщение записываем в файл:

WRITEBIN ("M_dec.txt","byte",0):= М*.

Шаг 15

Вычислим показатели визуального искажения, перечисленные в главе 3 (формулы (3.1)—(3.17)). Полученные результаты сведены в табл. 5.1 (стр. 125).