Основная теорема информационного скрытия при активном противодействии нарушителя
Исследуем скрытую пропускную способность (СПС) в случае активного противодействия нарушителя, который стремится разрушить скрыто передаваемую информацию. Информационно-скрывающее состязание между передающей и атакующей сторонами удобно описать методами теории игр [67, 68, 97]. В теории игр обычно идет речь о играх двух сторон (лиц); считается, что игры ограничены, то есть, оба играющих обоих случаях могут делать только определенное количество шагов, и игра заканчивается после ограниченного количества шагов. Отсюда вытекает ограниченность количества стратегий обоих играющих. Под понятием стратегии подразумевается такая система правил, с помощью которой задается действие (действия) игрока в определенной ситуации. Целью теории игр является нахождение лучшей стратегии отдельных игроков.
Цена игры в данном случае равна величине СПС, для максимизации которой отправитель информации оптимальным образом формирует скрывающее преобразование. Для минимизации СПС атакующий синтезирует оптимальное атакующее воздействие. Величина СПС может быть получена последовательным соединением скрывающего преобразования и атакующего воздействия. Для того чтобы оценить величину скрытой ПС для стеганосистемы с двоичным алфавитом, приведем исследования теоретико-игровых аспектов проблемы скрытия информации стеганосистемами.
Рассмотрим основную теорему информационного скрытия при активном противодействии нарушителя [61]. Для любых стеганосистем произвольной сложности и любых атак без памяти данная теорема ограничивает сверху скорость безошибочной передачи для скрывающего информацию при условии, что атакующий знает описание скрывающего преобразования, а получатель знает описания как скрывающего преобразования, так и атакующего воздействия. Данное условие на самом деле не является трудноосуществимым, как это может показаться на первый взгляд.
Даже если стратегии действий отправителя информации и атакующего неизвестны, но стационарны, то можно утверждать, что как атакующий, так и получатель потенциально способны их определить, обработав достаточно большой объем статистического материала. Это предположение совершенно реалистично, хотя и не всегда может быть достигнуто на практике, учитывая высокую вычислительную сложность [5].
Предварительно рассмотрим два утверждения, которые устанавливают области существования стеганосистем, потенциально способных безошибочно передавать скрываемую информацию при заданном атакующем воздействии [5].
В дальнейшем будем обозначать через H(x) энтропию переменной х, через I(х; у) — полное количество информации между х и у, а через 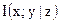 — условное полное количество информации между х и у, обусловленных z [68].
— условное полное количество информации между х и у, обусловленных z [68].
Утверждение 4.1
Зафиксируем атакующее воздействие  и изберем скрывающее преобразование
и изберем скрывающее преобразование 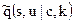 , которое максимизирует количество информации вида
, которое максимизирует количество информации вида
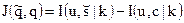 (4.10)
(4.10)
над  . Для любого сколь угодно малого значения
. Для любого сколь угодно малого значения 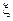 >0 и достаточно большого значения N существует стеганосистема с длиной блока N, которая обеспечивает вероятность разрушения скрываемых сообщений
>0 и достаточно большого значения N существует стеганосистема с длиной блока N, которая обеспечивает вероятность разрушения скрываемых сообщений  <
< 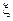 для множества скрываемых сообщений мощностью
для множества скрываемых сообщений мощностью

Утверждение 4.2
Пусть стеганосистема с длиной блока N способна безошибочно передавать скрываемые сообщения со скоростью  бит/элемент контейнера при атакующем воздействии
бит/элемент контейнера при атакующем воздействии  . Если для любого
. Если для любого 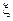 >0 стеганосистема обеспечивает вероятность разрушения скрываемых сообщений
>0 стеганосистема обеспечивает вероятность разрушения скрываемых сообщений  <
< 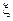 при
при 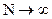 , то существует конечный алфавит U и такое скрывающее преобразование
, то существует конечный алфавит U и такое скрывающее преобразование  , что исполняется неравенство
, что исполняется неравенство

Теорема 4.1
Пусть атакующему известно описание обобщенного скрывающего преобразования  , а получателю известно описание обобщенного скрывающего преобразования
, а получателю известно описание обобщенного скрывающего преобразования  и обобщенного атакующего воздействия
и обобщенного атакующего воздействия  . Для любого информационно-скрывающего Состязания, приводящего к искажению не более, чем (А1,А2), скорость передачи R скрываемых сообщений достижима тогда и только тогда, когда
. Для любого информационно-скрывающего Состязания, приводящего к искажению не более, чем (А1,А2), скорость передачи R скрываемых сообщений достижима тогда и только тогда, когда  .
.
Величина В определяется как

где u — случайная переменная над произвольным конечным алфавитом U; переменные  образуют марковскую цепь, представляющую собой частную форму следующей марковской цепи:
образуют марковскую цепь, представляющую собой частную форму следующей марковской цепи:  , характеристики которой рассматриваются в [69]. Количество информации
, характеристики которой рассматриваются в [69]. Количество информации  определяется выражением (4.10).
определяется выражением (4.10).
Таким образом, теорема (4.1) определяет величину нижнего предела скрытой ПС в условиях, когда все участники информационного состязания знают стратегии действий друг друга. Необходимо отметить, что в данной теореме определяется величина СПС стеганоканала, о существовании которого атакующему известно. Данная СПС равна среднему количеству бит информации на один элемент контейнера, которую нарушитель не может разрушить, избирая любую стратегию противодействия из имеющегося множества  при искажении контейнера не более величины A2.
при искажении контейнера не более величины A2.
Доказательство этой теоремы сводится следующему. Зафиксируем атакующее воздействие  . В утверждении (4.1) указывается, что все скорости безошибочной передачн скрываемых сообщений, менее
. В утверждении (4.1) указывается, что все скорости безошибочной передачн скрываемых сообщений, менее  , достижимы.
, достижимы.
Утверждение (4.2) содержит обратный результат, то есть, достоверная передача выше этой скорости невозможна, поскольку атакующий осведомлен с распределением 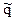 , которое минимизирует скорость передачи.
, которое минимизирует скорость передачи.
Далее показано, что в важном специальном случае, когда k=с (то есть, секретным ключом стеганосистемы является описание используемого контейнера, а сам контейнер известен получателю), нет потери оптимальности при ограничении кодера стеганосистемы видом, представленным на рис. 4.1.
Следствие
В случае k=c выбор значения переменной u оптимален тогда и только тогда, когда стеганосистема s может быть записана в форме s=Е(с, и), где отображение Е(с,u) обратно для всех значений с. В частности, выбор и=s оптимален. Скрытая ПС в этом случае определяется следующим образом:
 (4.12)
(4.12)
Это следует из того, что, когда k=с, выражение (4.10) может быть записано в виде
Следовательно, вполне логично, что величина скрытой ПС равна взаимной информации между стеганограммой s и искаженной стеганограммой  при условии, что отправителю и получателю скрываемой информации известен пустой контейнер с.
при условии, что отправителю и получателю скрываемой информации известен пустой контейнер с.
Для практических систем защиты информации, если секретным ключом стеганосистемы является описание используемого контейнера, возникают две проблемы [5], Во-первых, получатель должен знать контейнер-оригинал, что ограничивает возможную область применения таких стеганосистем. Во-вторых, отправитель и получатель скрываемых сообщений должны использовать секретную ключевую информацию очень большого объема, что не всегда удобно на практике.






