Рассмотрим выводы из теоремы (4.1) и комментарии свойства скрытой пропускной способности [5].
• Теорема (4.1) определяет, что установление теоретической вероятности скрытой безошибочной передачи информации и теоретической вероятности противодействия этому сводится к вычислению величины СПС В при известных стратегиях сторон и сравнению ее с необходимой скоростью передачи скрываемой информации R. Если СПС окажется меньше необходимой скорости, то даже теоретически не существует способа передачи скрываемых сообщений без искажений, и задача атакующего относительно разрушения произвольных стеганосистем гарантированно будет решаться.
Оптимальная атака нарушителя заключается во внесении такого искажения А2, при котором величина СПС меньше необходимой скорости передачи скрываемых сообщений. Оптимальная стратегия скрывающего информацию сводится к избранию такого кодирования и такой величины вызванного им искажения А1, при которых с учетом искажения А2 необходимая скорость безошибочной передачи не будет превышать СПС. Это означает, что теоретически существует такой способ безошибочной передачи. Однако теоретическая возможность еще не означает, что передающая сторона будет способна реализовать ее на практике. Например, разработчик стеганосистемы может не знать оптимальных принципов ее построения (они еще не открыты), или из-за ограниченности в вычислительных ресурсах он не может себе позволить оптимальную обработку, или требования к своевременности доставки скрываемых сообщений ограничивают длину N блока кодирования и т.п.
Таким образом, успех любой из состязающихся сторон в окончательном итоге будет определяться соотношением между скоростью передачи R и величинами искажения А1 А2 контейнера, в котором скрывается информация.
Рассмотренная теорема информационного скрытия при активном противодействии нарушителя напоминает фундаментальную теорему Шеннона (С. Shannon), в которой определяется, что существует способ безошибочной передачи сообщений по каналу с помехами, если Скорость передачи меньше пропускной способности канала, и невозможна достоверная передача со скоростью, превышающей пропускную способность канала. Шеннон также показал, что существуют зависимости между отношением мощности полезного сигнала к мощности помех в канале связи и величиной скорости безошибочной передачи сообщений по этому каналу. Аналогично этому, в информационно-скрывающем состязании существуют подобные зависимости между отношениями величин искажения кодирования А1 к величине искажения атакующего воздействия A2 и величиной скорости безошибочной передачи скрытых сообщений по стеганоканалу. Но при внешнем сходстве, у задач открытой и скрытой передачи есть существенные отличия. Открытая связь осуществляется в условиях влияния случайных помех канала связи, а передача скрытой информации должна быть обеспечена даже в условиях оптимизированного намеренного противодействия активного нарушителя.
• Рассмотрим связь задачи информационного скрытия с задачей защиты информации от перехвата в прослушиваемом канале. В 1975 г. американский ученый Вайнер (A.D. Wyner) предложил метод защиты информации от чтения нарушителем, что заложило основы теории кодового зашумления [5, 71-73]. Отправитель дискретных сообщений выполняет их случайное избыточное кодирование и передает преобразованные сообщения получателю основным каналом связи. Нарушитель наблюдает их в подслушивающем канале, который является отводом от основного канала. Случайное кодирование построено таким образом, что если в подслушивающем канале есть ошибки, то при декодировании они размножаются и надежно искажают защищаемую информацию.
Метод кодового зашумления предназначен для систем передачи, в которых основной канал безошибочен. Например, основной канал образован на основе волоконно-оптической линии, а нарушитель пытается вести разведку по каналам побочного электромагнитного излучения и наводок, в которых, в силу их природы, существует большое количество -помех. Отметим, что нарушитель знает описание системы кодового зашумления, которая не использует секретной ключевой информации (некриптографический способ защиты).
Подслушивающий канал характеризуется секретной ПС, представляющей собой максимальную скорость безошибочной передачи основным каналом при условии, что неопределенность для перехватчика максимальна (неопределенность защищаемых сообщений равна энтропии этих сообщений). Однако, если подслушивающий канал менее зашумлен по сравнению с основным каналом, то секретная ПС равна нулю.
В задаче информационного скрытия атакующий способен на большее, чем обыкновенный перехватчик в подслушивающем канале, поскольку он после перехвата защищаемого сообщения умышленно искажает основной канал. Поэтому основной канал передачи не менее зашумлен, чем подслушивающий. Следовательно, в задаче информационного скрытия с активным нарушителем секретная ПС равна нулю.
• Избрание переменной и независимо от контейнера с, как это реализовано в системе ЦВЗ [5], в общем случае неоптимально. Анализ выражения (4.10) показывает, что скорости безошибочной передачи в этом случае ограничены сверху величиной  .
.
• Пусть выполняется условие  Если атакующему известно описание контейнера сN, то оптимальная атака заключается только в формировании искаженной стеганограммы в виде
Если атакующему известно описание контейнера сN, то оптимальная атака заключается только в формировании искаженной стеганограммы в виде  . В этом случае выходной сигнал после атаки не содержит никаких следов сообщения, и скрытая ПС равна нулю. На практике это может означать следующее. Если нарушителю не известен оригинал защищаемой от пиратского копирования информации, то никакие стеганосистемы не защитят авторские или имущественные права производителей этой информации.
. В этом случае выходной сигнал после атаки не содержит никаких следов сообщения, и скрытая ПС равна нулю. На практике это может означать следующее. Если нарушителю не известен оригинал защищаемой от пиратского копирования информации, то никакие стеганосистемы не защитят авторские или имущественные права производителей этой информации.
Рассмотрим потенциально сильную атаку, в которой атакующий стремится сконструировать достаточно близкую к оригиналу оценку контейнера сN. Если атакующий способен синтезировать искаженную стеганограмму  такую, что,
такую, что,  то СПС будет ограничиваться сверху величиной
то СПС будет ограничиваться сверху величиной
 (4.14)
(4.14)
для любого и. Следовательно, величина скрытой ПС стеганоканала  .
.
Таким образом, если нарушитель способен сформировать достаточно точную 'оценку контейнера (другими словами, выполняется неравенство  где величина
где величина 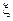 достаточно мала), то значение СПС ограничено этой малой величиной. Ha практике это означает, что, имея заполненный контейнер (стеганограмму), нарушитель может попытаться воссоздать из него с некоторой допустимой погрешностью контейнер-оригинал, из которого изъято скрытое сообщение (это особенно актуально в области защиты с помощью ЦВЗ мультимедийной информации).
достаточно мала), то значение СПС ограничено этой малой величиной. Ha практике это означает, что, имея заполненный контейнер (стеганограмму), нарушитель может попытаться воссоздать из него с некоторой допустимой погрешностью контейнер-оригинал, из которого изъято скрытое сообщение (это особенно актуально в области защиты с помощью ЦВЗ мультимедийной информации).






