Часть 2. Введение в теорию вероятностей и математическую статистику
Глава 1. Случайные события
Понятие случайного события.
Модели экспериментов со случайными исходами
Математическая формализация модели сл. эксперимента
1. Построение множества элементарных исходов W
2. Описание поля событий Á для данного эксперимента
3. Задание вероятностного распределения на Á
Аксиоматическая теория вероятностей – Колмогоров, 1933
А произошло (наступило, осуществилось, реализовалось) wÎА
Æ - невозможное, W - достоверное. Совместные события, несовместные события
Алгебраические операции над событиями.
А Ì В влечет за собой А = В Û А Ì В и В Ì А
Сумма А + В хотя бы одно из Произведение А.В совместное осуществление
Разность А – В А происходит, В нет 
противоположное
А + В = В + А, А.В = В.А (А + В) + С = А + (В + С), (А.В).С = А.(В.С) (А + В).С = А.С + В.С
Аксиоматическое определение вероятности события.
Á Р(А) "АÎÁ Аксиомы 1) Р(А) ³ 0 2) Р(W) = 1 3) А1, А2, …, Аn, … Ai.Aj = Æ (i¹ j)
íW, Á, Pý вероятностное пространство сл. эксперимента
1) Р(Æ) = 0 2) 
3) Р(А) £ 1 4) А Ì В Þ Р(А) £ Р(В) 5) А = В Þ Р(А) = Р(В)
6) Р(А + В) = Р(А) + Р(В) – Р(А.В) формула (теорема) сложения вероятностей
Классическая вероятностная схема (схема урн).
конечное число равновозможных исходов (Р(w1) = Р(w2) = … = Р(wN) = 1 ¤ N)
Комбинаторный метод вычисления вероятностей в классической схеме.
Выбор k элементов из n
без возвращения (повторения) с возвращением (повторением)
Элементы по мере выбора
упорядочиваются не упорядочиваются упорядочиваются не упорядочиваются
1. 2. 3. 4.
1. Схема выбора, приводящая к размещениям 
k = n 
число перестановок
Схема выбора, приводящая к сочетаниям
биномиальные коэффициенты
3. Схема выбора, приводящая к размещениям с повторениями N(W) = nk
4. Схема выбора, приводящая к сочетаниям с повторениями 
Геометрические вероятности. Задача о встрече.
wÌW А = í(х,у)Îwý 
О статистической вероятности.
относительная частота 
Условные вероятности. Независимость событий.
A и B P(A) > 0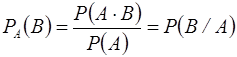 
осуществления события В при условии, что А произошло
«вероятность В при условии А» А наз. независимым от В, если РВ(А) = Р(А)
А и В наз. независимыми, если Р(А.В) = Р(А).Р(В)
§9. Вероятности сложных событий. Вероятность «хотя бы одного события».
Р(А.В) = Р(А).РА(В) = Р(В).РВ(А) формула умножения вероятностей
Р(А + В) = Р(А) + Р(В) – Р(А.В) формула сложения вероятностей
Р(А.В.С) Р(А + В + С)
Формула полной вероятности.
H1, H2, …, Hn наблюдаемые система множеств í H1, H2, …, Hn ý разбиение W 
гипотезы по отношению к А доопытные (априорные)
§11. Формула Байеса. (Bayes)
Эксперимент проведен и событие А осуществилось послеопытная (апостериорная)
