Методика изучения табличного умножения и деления
Изучение таблицы умножения и деления является центральной задачей обучения математике во 2 и 3 классе. Результаты табличного умножения в соответствии с программными требованиями к знаниям, умениям и навыкам дети должны знать наизусть. Умножение с числом нуль, с числами 1 и 10 относятся к особым случаям.
К табличному умножению относятся случаи умножения однозначных натуральных чисел на однозначные натуральные числа, результаты которых находят на основе конкретного смысла действия умножения (находят суммы одинаковых слагаемых).
1. Умножение двух — первый этап в рассмотрении табличных случаев умножения.
Результат 2х2 = □ находят действием сложения, помня, что умножение — это сумма одинаковых слагаемых. Поэтому, 2 + 2 = 4. Следовательно, 2 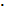 2 = 4.
2 = 4.
Аналогично:
 = 6,
= 6,  2 + 2 + 2 = 6,
2 + 2 + 2 = 6,
 2 + 2 + 2 + 2 = 8,
2 + 2 + 2 + 2 = 8,
 2 + 2+ 2 + 2 + 2 = 10,
2 + 2+ 2 + 2 + 2 = 10,
Для остальных случаев используется предыдущий результат:
 , 10 + 2 = 12, следовательно,
, 10 + 2 = 12, следовательно, 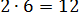 ,
,
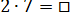 , 2
, 2  5 = 10, 10 + 4 = 14, следовательно, 2
5 = 10, 10 + 4 = 14, следовательно, 2  7 = 14.
7 = 14.
2. Умножение на число 2 (таблица составляется на основе переместительного свойства умножения):
| 2 х 2 = 4 2 х 3 = 6 2 х 4 = 8 ………. | 3 х 2 = 6 4 х 2 = 8 ……… |
3. Табличное деление рассматривается на основе взаимосвязи умножения и деления следующим образом:
если 3  2 = 6, то 6:2=3 и6: 3 = 2.
2 = 6, то 6:2=3 и6: 3 = 2.
Решение записывают столбиком:
7 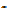 2 = 14; 6
2 = 14; 6 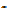 2 = 12;
2 = 12;
14:2 = 7; 12: 2 = 6;
14: 7 = 2. 12: 6 = 2.
Таким образом, приходим к таблицам умножение числа 2 и умножение на число 2. Затем на основе связи между умножением и делением находятся соответствующие случаи деления:
| 2 х 2 = 4 2 х 3 = 6 2 х 4 = 8 2 х 5 = 10 2 х 6 = 12 2 х 7 = 14 2 х 8 = 16 2 х 9 = 18 | 3 х 2 = 6 4 х 2 = 8 5 х 2 = 10 6 х 2 = 12 7 х 2 = 14 8 х 2 = 16 9 х 2 = 18 | 4: 2 = 2 6: 2 = 3 8: 2 = 4 10: 2 = 5 12: 2 = 6 14: 2 = 7 16: 2 = 8 18: 2 = 9 | 6: 3 = 2 8: 4 = 2 10: 5 = 2 12: 6 = 2 14: 7 = 2 16: 8 = 2 18: 9 = 2 |
Таблица умножения каждого числа начинается с умножения этого числа на число, равное ему. Так, таблица умножения числа 4 начинается с умножения 4 х 4, потому что предыдущие случаи 4 х 2 и 4 х 3 уже усвоены, когда изучались таблицы умножения чисел 2 и 3.
Знание таблицы умножения и соответствующих случаев деления доводится до автоматизма.
Умножение и деление с 0 и 1
Случаи умножения и деления с 0 и 1 считаются особыми и рассматриваются отдельно от табличных случаев умножения и деления, поскольку они не могут быть разъяснены с общих позиций смысла действий умножения и деления.
Умножение единицы на любое число рассматривается на основе определения умножения как суммы одинаковых слагаемых. Например, 1x5 = 1 + 1 + 1 + 1 + 1 = 5. Этот случай не вызывает трудностей.
Умножение любого числа на 1, умножение любого числа на нуль вводится как особый, его нельзя ввести на основе определения умножения. Поскольку фраза: «повторяем слагаемым 1 раз» или «повторяем слагаемые 0 раз» не имеет смысла, на общее определение в этом случае не ссылаются, а просто вводят эти случаи по соглашению, т. е. сообщают детям, что при умножении любого числа на 1получаем то же число; при умножении любого числа на нуль, получаем в произведении нуль.
В программах Л.Г. Петерсон, Н.Б. Истоминой эти случаи вводятся на основе переместительного свойства умножения.
Деление на единицу рассматривается на основе связи между умножением и делением. Например, 3:1=3, так 1х 3 = 3. В общем виде закономерность оформляется в буквенном виде: а: 1 = а, так как 1 х а = а (при делении числа на 1,получается то же самое число).
Случай вида а: а = 1, если а ≠ 0, вводится также на основе связи деления с умножением (при делении числа на то же самое число вчастном получается 1).
Например, 7:7 = 1, так как 1x7 = 7.
Деление нуля на любое число рассматривается на основе связи деления с умножением.
Например, 0:3 = 0, так как 0 х 3 = 0. В общем виде закономерность оформляется в буквенном виде: 0:b = 0 (при делении нуля на любое число, отличное от нуля, а частном получается нуль).
Невозможность деления на нуль может быть обоснована ссылкой на связь умножения с делением примерно так: «Если бы мы захотели решить пример типа: 6: 0,то нужно было бы подобрать такое число в частном, при умно женим которого на нуль получилось бы 6.Но при умножении любого числа на нуль — всегда получается нуль. Значит, найти такого числа нельзя. Следовательно, и делить на нуль нельзя».






