Задача такая: имеется искаженная картина (изображение), для которой известны точные значения координат 4-х точек. Необходимо восстановить ее действительное изображение. Для этого по 4-м известным точкам восстанавливают исходную систему координат а значит и правильную геометрическую форму объекта.
Итак, имеется 4-е исходные точки и надо получить матрицу перехода вперёд и назад. Прямое преобразование было уже получено и приведено выше – слайд 23. Необходимо получить коэффициенты перехода в обратную сторону и получить, таким образом, матрицу обратного преобразования.
Сразу заметим, что коэффициент а33 = 1, и его искать не надо. Его можно сократить в числителе и знаменателе (просто вынести за скобку). Соответственно, в системе уравнений число уравнений будет не 9, а 8. Заметим также, что в формулах аффинного преобразования отсутствовал знаменатель, т.к. координата w всегда была равна 1 для точки (радиус-вектора) и 0 для направления, а коэффициенты p и q равнялись нулю. В перспективном преобразовании p и q не равны 0.
Решение задачи. Имеется 4-е точки соответствия стартового изображения и перспективного. Отметим, что в похожей задаче аффинного преобразования таких точек требовалось 3. Нужно найти такую матрицу, которая будет давать точный переход из одной системы координат в другую. Решение будем искать в виде
Р = Р' ∙ М; М=?
или
М = Р ∙ (Р')-1,
где М - матрица обратного преобразования.
Исходные данные: имеется 4-е пары точек соответственно в одной СК и в другой:
| (х0 у0) | ↔ | (х'0 у'0) |
| (х1у1) | ↔ | (х'1 у'1) |
| (х2 у2) | ↔ | (х'2 у'2) |
| (х3 у3) | ↔ | (х'3 у'3) |
Если в итоговой формуле для координат – слайд 23, умножить левые и правые части на знаменатель, помня, что в аффинных преобразованиях W=1 и a33=1, то получим два уравнения:
x=a11x'+a21y' +a31-a13x'x-a23y'x;
у=a12x+a22y' +a32-a13x'x-a23y'y;
Это зависимость новых координат от старых.
Подставляя в эти уравнения значения исходных координат как 8 зависимостей заданных пар точек, получим 8 уравнений для нахождения коэффициентов матрицы преобразования. В матричной форме эти линейные уравнения приведены на слайде 26.

Задачу решения этих уравнений можно упростить, не применяя метод Гаусса. Суть такого решения состоит в том, что вместо прямого преобразования переход из одной системы координат в другую можно найти через единичный квадрат – слайд 27, координаты вершин которого:
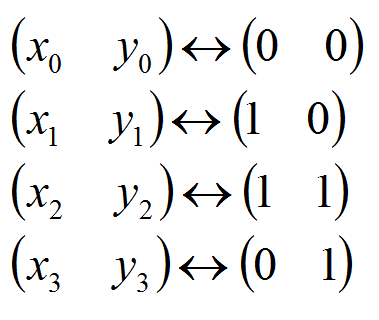
показаны на рис. ниже

Подставляя эти координаты в матрицу М1 и в матрицу М2 в итоговом матричном уравнении получим много нулей, что упростит все вычисления. Разобьём задачу на две части. Найдём матрицу М1 преобразования заданного изображения в единичный квадрат. Затем выполним ту же операцию с преобразованным четырёхугольником и получим матрицу М2. Тогда искомая матрица М может быть определена через скалярное произведение матриц М1 и М2, т.е. М = М1 ∙ М2-1.
Из матрицы М1 получаем уравнения для определения неизвестных коэффициентов a ij
а11=х1-х0+а13х1
а21=х3-х0+а23х3
а31=х0 эта система получена из исходной, слайд 27
а12=у1-у0+а13у1
а22=у3-у0+а23у3
а32=у0
Для решения уравнений относительно коэффициентов a ij (слайд 27 и 29) можно ввести обозначения:
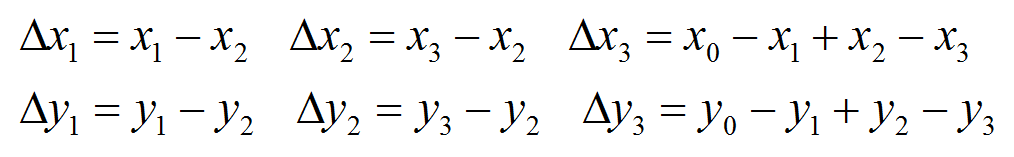
И дальше находим решение (методом Крамера) для коэффициентов, отвечающих за перспективное преобразование:
a13= 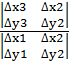 a23=
a23= 
В результате получается матрица М1 перехода из исходного четырёхугольника в единичный квадрат.
Все процедуры повторяют для второй фигуры и получают матрицу М2. В конечном итоге получают матрицу М, обеспечивающую универсальный механизм произвольной привязки координат.
С плоскостью всё.
Это преобразование можно использовать для целей создания перспективных преобразований изображений, а также исправления разного рода искажений, на кривой фотографии или плохо отсканированной книги. Если исходная фигура была параллелограммом, то коэффициенты а12 и а13 получим равными 0, так как преобразование будет аффинным.






