Как можно догадаться - с пространством всё тоже самое, что и с плоскостью. Все правила, которые касались АП в однородных координатах на плоскости, сохраняются и в пространстве, все проблемы, что были на плоскости, остаются и в пространстве. Можно предположить, что все эти правила действительны и для любого n-мерного пространства. Что надо хорошо помнить: есть разные понятия: радиус-вектор по сути – это точка в КГ, а свободный вектор – это просто направление, и третье понятие – нормаль. Преобразования для них определяют по-разному. В пространстве всё также, причём в пространстве это более актуально, т.к. в трёхмерной графике много задач, которые не часто или вообще не встречаются на плоскости.
Итак, в пространстве имеем три координаты x,y,z и дополнительно вводится координата W для получения свойства однородности. Также для АП принимаем, что W=1 и тогда (x, y, z) = ( ,
,  ).
).
Преобразования в общем случае можно представить в виде скалярного произведения вектора – строки на матрицу преобразования – слайд 29:

В матрице 12 коэффициентов. Блок (3х3) (как в 2D блок (2х2)) отвечает за преобразования - поворот, масштабирование… Нижняя строка отвечает за параллельный перенос, правый столбик должен отвечать за перспективные преобразования, но пока эти вопросы рассматривать не будем. Матрицы преобразования имеют аналогичный вид и смысл - (слайд 30)

и повороты - (слайд 31)

Если вспомнить пример поворота точки, то в пространстве выполнить это так же просто нельзя. Поворот, рассмотренный на плоскости, по существу был выполнен вокруг оси Z, и если надо выполнить поворот какой-то точки в пространстве, то его нельзя задать однозначно простым действием. Он будет описываться посредством трёх матриц – вокруг оси Z, оси Х, оси У, т.е. его надо будет разбить на ряд отдельных действий – на три составных.
Ещё одно замечание – определитель матрицы равен 1. Это означает, что в процессе поворота объект не поменяет своих размеров и не претерпеет какой-либо деформации, т.е. ведёт себя как твёрдое тело. Этому телу можно задавать необходимую ориентацию в пространстве. Тоже можно сказать и о параллельном переносе.
Имеется более универсальный способ осуществления поворота относительно произвольной оси, проходящей через начало координат. Матрица такого преобразования построена на КВАТЕРНИОНАХ и приведена ниже:

С кватернионами следует познакомиться самостоятельно!
Замечание о кватернионах.
При выводе последнего соотношения использовалось понятие о кватернионах. Это система гиперкомплексных чисел (предложена в 1843 г. Гамильтоном, в то время - гл. астрономом Англии).
Кватернион – это пара (а, ū). а - скаляр, вещественное число. ū - вектор трёхмерного пространства. Кватернионы образуют систему (ряд) гиперкомплексных чисел, подобную другим числовым рядам. Если коротко – то это 4-х компонентная математическая абстракция со своими свойствами и правилами выполнения операций сложения и умножения. Кватернион в общем виде можно представить как сумму a+bi+cj+dk, где a,b,c,d – вещественные числа, а i,j,k – несократимые мнимые единицы, причём для них определено, что
i2=j2=k2=ijk= -1;
и
ij=k, ji= - k.
Примеры числовых рядов:
Натуральные: 1,2,3,4,5….
Целые: 0,1,-1,2,-2,…
Рациональные: 1;-1;1/2; 0,12,..
Вещественные: рациональные + ирац.: π, е,  ,….
,….
Комплексные: -1; ½; π; 3i+z; -еiπ/3;… (включают в себя все предшедствующие)
Кватернионы: 1; -1; 1/2; I; j; k; πj-1/2k; …
На сегодня можно считать, что кватернион – универсальное число, определяющее любую точку видимого пространства.
9. Пример трёхмерного преобразования – построение матрицы камеры -(слайд 34)
Достаточно часто требуется изменение наблюдения на сцену. Т.е. имеется некоторая сцена и требуется изменить наблюдение на эту сцену с помощью матрицы трёхмерного преобразования.
Считаем, что виртуальный наблюдатель (камера) находится в некоторой точке “C” в ортогональной системе координат U,V,N

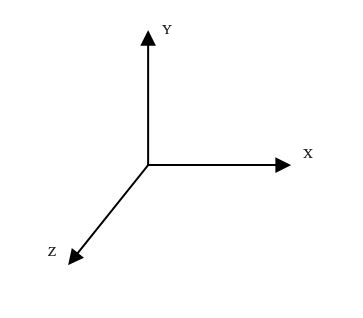
и есть другая система координат – X,Y,Z (мировая). Мировые координаты описывают истинное положение объектов в пространстве. Экранная система координат предназначена для синтеза (создания) изображения на к.-л. плоскость. Эта система может быть двумерной и трёхмерной. Различают так же другие системы координат как системы устройств изображения, осуществляющие вывод изображения в заданной форме.
Проекция - способ отображения объекта на графическом устройстве: экране, бумажном, тканном или другом материальном носителе на плоскости или поверхности.
Будем считать, что обе системы координат правосторонние, и та, что в камере и мировая. Это означает, что ось Z смотрит на нас. Все векторы направлений нормированы и, что естественно, ортогональны. Это требуется для сокращения набора вычислений. Камеру С должно рассматривать как некоторую одноразовую, однократно задаваемую в программе абстракцию. Её можно заранее настроить, а затем применить ко всем объектам.
Что значит настроить? Настроить – это значит ортонормировать все векторы и согласовать их с векторами – направлениями в другой СК. А дальше применять так долго, как это потребует обстановка.
Что будем искать? Будем искать такое преобразование, которое переводит объект из мировой системы координат в систему координат наблюдателя.
Как будем делать?
Сначала перенесём камеру в начало координат Мировой СК на (- Cz), (- Cy), (- Cx); затем повернём, причем таким образом, что бы оси -U совпала с осью X, V совпала с осью Y и ось N c осью Z; т.е. будем искать матрицу преобразования в виде: перенос-поворот.
Поскольку камера находится в позиции точка “C” с координатами (x,y,z), то необходимо выполнить обратный её перенос: матрица переноса показана на слайде 33.

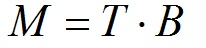
где Т – матрица переноса

Второе действие - это поворот. Поворот необходимо выполнить так, чтобы ось Х МСК совпадала с осью U, ось Y - c осью V и ось Z с осью N. Матрица “B” (см. ниже) должна давать то, что находится в матрице поворота справа – слайд 34.
После преобразования «перенос» векторы (так как они ортонормированны) отобразятся:

Т.е исходное преобразование представляется в развернутом матричном виде как
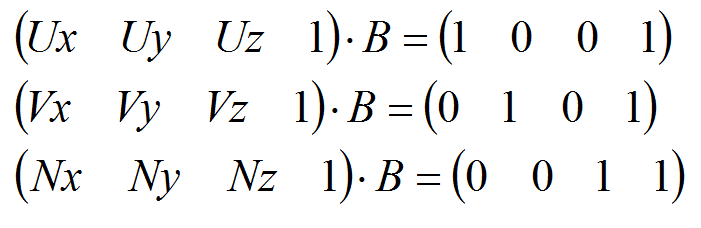
Так как в матрице скалярно перемножаются взаимно-перпендикулярные векторы, то в результирующей матрице будет получаться 0, а при умножении вектора на самого себя будем получать единицу. Последний столбец имеет только единицы, т.к. выполняется аффинное преобразование. Исходя из сказанного можно определить и компоненты матрицы В, не выполняя вычислений → слайд 35.
Зная, что

Находим матрицу поворота В:

Если бы вектор N был направлен в противоположную сторону, то в правом предпоследнем столбце компоненты Nx, Ny и Nz должны были иметь знак “-”.
Что с этим делать потом? Дальше это используют для передачи образа, который находиться в камере на некоторый экран после дополнительных преобразований – масштабирования, отсечения линий, которые не войдут на экран и др.
В этой теме были использованы методические разработки В.Галинского.






