Существуют еще два вида преобразований – ПЕРСПЕКТИВНОЕ И БИЛИНЕЙНОЕ
Перспективное преобразование - это попытка имитации перспективы объекта, сцены, некоторого пространства при изображении этих объектов на плоскости. Например, при взгляде на кирпичное здание та часть его, которая к нам ближе представляется выложенной более крупным кирпичом, а та, что дальше – менее крупным. При этом прямолинейность сохраняется, а параллельность линий в направлении взгляда – нет. После преобразования прямоугольника, его диагонали остаются прямыми, а параллельные линии будут пересекаться в некоторой точке, называемой точкой схода рис. ниже.

Что при этом произошло? Параллельность нарушена, а во внутренней области произошли искажения (деформации) картинки. Искажения внутри картинки видны на слайде 19 – изменились расстояния между отдельными квадратиками, размеры самих квадратиков, нет параллельности линий.


Изображение выглядит более корректно по сравнению с картинкой после АП. Перспективное преобразование применяют для получения имитации объемного изображения и как передачи перспективы на плоскости, а также для текстурирования изображения. Однако если делать ворпинг, то возникнуть проблемы в стыке – как на рис. выше этого текста. В частности - соотношение размеров рисунка по всей плоскости изменилось, и нет безупречного стыка.
Ø Альтернатива всему этому –
Ø билинейное преобразование.
Дополнительно оно сглаживает изображение и делает его более реалистичным. В чем суть билинейного преобразования?


Всю зону четырехугольника разбивают по сторонам на одинаковое количество частей, причем длины этих частей равны. Противоположные части разбиения по сторонам мысленно соединяют отрезками. Тогда после преобразования и ворпинга получаем изображение, в котором отсутствуют дефекты на стыке двух частей и отсутствуют дефекты искажения внутри изображения, как это видно на рис.
Что происходит? А происходит следующее. Возьмем некоторую область и выделим в ней 4-х угольную зону, причем зона может быть абсолютно любой – не обязательно как на рис. ниже. Обозначим вершины 4-х угольника символами P0, Р00, Р1, Р11 и на каждой стороне выделим текущую точку r0 внизу и r1 вверху. Преобразования выполняют путем линейной интерполяции положения точек четырехугольника (его вершин). Для этого r0 и r1 связывают с соответствующей стороной линейными зависимостями

r0 = P0(1-t) + P00t
r1 = P1(1-t) + P11t,
где t – интерполяционный шаг, (иначе – параметр сканирования), который задается в интервале значений 0 <= t <= 1. По вертикали одновременно перемещается результирующая точка q в соответствии с уравнением
q = r0(S1-1) + r1S, причем, параметр s изменяется в таком же интервале, 0 <= S <= 1, но величина шага может и не равняться шагу t/
С одной стороны идет интерполяция по t, а с другой, в поперечном направлении по S – это и будет билинейной интерполяцией. И если t и S изменяются от 0 до 1, то в процессе преобразования исходного четырехугольника произойдет сканирование всех его точек. Изменяя шаги t и S по величине можно получать изображения разного качества. Для небольшой точности изображения необходимо, чтобы число шагов было не хуже количества растровых точек, которые оказались в этом прямоугольнике. Если требуется улучшить изображение, то можно увеличить это число. Но в этом случае возникает проблема. Так как картинка дискретная, то во время прохождения по зоне потребуется некоторые точки учитывать несколько раз. То-есть каждый пиксель будет разбиваться на несколько частей. Этот вопрос решают, задавая каждой точке некоторый весовой коэффициент – то-есть сколько раз надо сохранять точку цветной и для каждой точки должен быть счетчик. Счетчик позволяет получить усредненное и более точное значение цвета для этой точки, так как будет учитываться не только данная точка, но так же и сведения о тех точках, которые только касаются этого пикселя. В результате происходит сглаживание изображения, и как бы уменьшается его дискретность. Недостаток такого подхода очевиден – очень большое время работы. Решение очевидно. Требуется искать компромисс между скоростью и качеством работы. Чаще всего предпочтение отдается скорости.
7.4 Перспективные преобразования (дополнение)
Если рассмотреть процесс использования правого столбца матрицы АП, то оказывается, что именно коэффициенты правого столбца, их применение приводят к эффекту перспективного преобразования - слайд 22 – рис ниже.
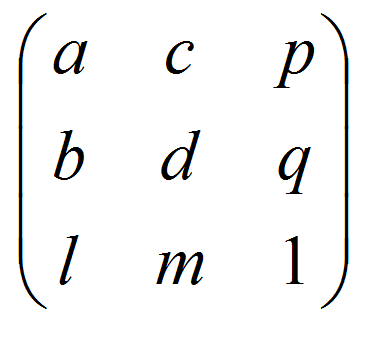

В обще случае матрица преобразований может быть записана в однородных координатах, как состоящая из 9 коэффициентов не равных одновременно нулю, слайд 23. Общая формула перспективного преобразования (прямое отображение) записывается в виде

Задача заключается в нахождении этих коэффициентов. Уравнение прямого алгебраического отображения при W не равного нулю соответственно имеют вид
x=x’a11+a21y’+a31w’
y=x’a12+a22y’+a32w’
w=x’a13+a23y’+a33w’
Полагая, что w=1 (всегда для отображения на плоскости) и поделив обе части всех уравнений на третье уравнение получим итоговую формулу для координат
 =
= 

Здесь a13x'+a23y'+a33 – нормирующий множитель, дающий это искажение, (слайд 22). В общем случае для единичного квадрата на плоскости искажение получим как на рис. ниже

Появление коэффициентов a13 и a23 (p, q) вызывает нарушение (иначе – исчезновение) параллельности.
Надо помнить, что коэффициент a33 = 1, и его не требуется находить. Таким образом, число неизвестных коэффициентов уменьшается до 8.
Перспективное преобразование очень важное. Оно позволяет передать эффект объемности объекта на плоскости, а также восстановить объект, который претерпел какие-то изменения, например, когда из некоторой правильной фигуры была получена искаженная - фото, картография, и применяя перспективное преобразование вполне возможно получить первоначальную картинку без искажения, что нельзя исправить аффинным преобразованием, но если известны 4 координаты действительного изображения.






