Пусть опорная часть вала – цапфа, вращающаяся в подшипнике скольжения, прижимается к подшипнику силой 
(рис. 11). Со стороны подшипника на вал в некоторой точке 
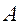при этом будет действовать нормальная реакция 
, являющейся равнодействующей всех элементарных сил давлений, распределенных на поверхности соприкосновения цапфы и подшипника. В этой же точке 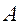будет действовать сила трения 
, направленная по касательной к окружности цапфы против вращения.
Рис.11
Складывая нормальную реакцию и силу трения , получим полную реакцию 
, которая равна по величине, но направлена противоположно силе . Реакция отклонена от нормали на угол трения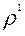 
. Этот фиктивный (приведенный) угол трения отличается от действительного 
для материалов вала и подшипника и зависит от закона распределения давления.
Закон распределения давления на соприкасающихся поверхностях принимают:
а) для новых неприработавшихся цапф и подшипников удельное давление является величиной постоянной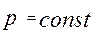 
(рис. 12,а);
б) для приработавшихся цапф и подшипников удельное давление распределяется по закону 
(рис.12,б).
Учитывая указанные законы распределения давления, фиктивные коэффициенты трения будут равны:
Для не приработавшихся цапф 
;
Для приработавшихся цапф 
.
Фиктивный угол трения 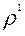равен
= 
.
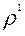Рис.12
Реакция (рис.11) создает относительно оси момент сопротивления (момент трения)
,
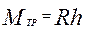направленной противоположно движущему моменту 
. Величина плеча 
, как видно из рисунка, равна
= 
,
где 
-радиус опорной части вала.
Так как угол трения очень мал, то
.
Следовательно
= 
. (15)
Тогда момент сил трения равен
(16)
Итак, полная реакция проходит при учете сил трения не через ось вращения вала, а отстоит от нее на расстоянии , т.е. является касательной к окружности радиусом . Эта окружность называется кругом трения.
