Задание 8. Выборочный метод. Точечные и интервальные оценки параметров распределения

Для изучения некоторого количественного признака генеральной совокупности получена выборка. Необходимо:

1) задать статистическое распределение выборки в виде интервальной таблицы частот;

2) построить гистограмму частот и полигон относительных частот (на разных рисунках);

3) найти эмпирическую функцию распределения и построить ее график;

4) найти несмещенные оценки математического ожидания и дисперсии генеральной совокупности ;

5) используя критерий согласия Пирсона (), проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости ;

6) найти доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения генеральной совокупности с надежностью .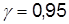

8.1.	8,3	7,2	6,2	6,7	7,3	5,7	7,7	8,2	6,1	7,2	5,3
	6,3	5,4	8,2	7,5	6,2	5,9	6,2	6,7	5,2	7,4	6,5
	7,1	6,7	7,3	6,2	7,2	6,6	6,5	5,7	6,0	6,7	7,9
	5,7	6,7	7,0	6,9	4,7	8,7	4,2	4,7	8,7	6,2	6,7
	5,1	6,5	6,7	5,2	8,9	5,5	7,1	6,8	4,9	8,1	5,8

 

8.2.

 

8.3.

8.4.

 

8.5.

 

8.6.

 

8.7.	1,22	1,13	1,16	1,12	1,01	1,06	1,05	1,10	1,11	1,13	1,20
	1,08	1,10	1,15	1,11	1,02	1,04	1,07	1,22	1,14	1,05	1,07
	1,13	1,14	1,15	1,06	1,22	1,19	1,13	1,12	1,16	1,19	1,17
	1,15	1,16	1,13	1,10	1,14	1,19	1,21	1,17	1,18	1,23	1,10
	1,03	1,04	1,10	1,10	1,19

 

8.8.

 

8.9.

 

8.10.
8.11.	0,90	0,94	0,84	0,86	0,88	0,90	0,92	0,89	0,85	0,91	0,89
	0,80	0,87	0,89	0,88	0,78	0,84	0,81	0,85	0,95	0,94	0,86
	0,86	0,91	0,78	0,82	0,91	0,95	0,97	0,88	0,83	0,82	0,84
	0,82	0,87	0,94	0,90	0,96	0,94	0,89	0,87	0,99	0,85	0,91
	0,80	0,90

 

8.12.	0,90	0,88	0,79	0,86	0,93	0,96	0,98	0,96	0,90	0,92	0,94
	0,93	0,91	0,86	0,92	0,91	0,94	0,90	0,86	0,90	0,93	0,90
	0,95	0,99	0,91	0,84	1,00	0,83	0,93	0,95	0,96	0,91	0,99
	0,85	0,97	0,90	0,93	0,95	1,00	0,83	0,85	0,87	0,90	0,89
	0,92	0,88	0,97	0,91	0,92

 

8.13.

 

8.14.

 

8.15.

 

8.16.

 

8.17.	19,1	18,1	18,4	18,2	19,5	19,7	19,0	19,7	19,1	19,2	18,4
	18,5	18,3	18,7	19,2	19,1	18,5	19,7	19,1	19,7	19,3	19,5
	18,2	18,7	19,4	19,3	18,5	18,6	18,8	19,1	18,7	19,1	19,6
	18,8	19,1	19,0	19,5	19,3	18,8	19,0	19,3	18,9	19,0	19,8
	19,3	19,2	18,6	19,9	18,7	20,0	19,5	18,8

 

8.18.	20,8	20,8	20,0	19,8	20,0	20,2	20,4	20,8	19,6	19,9	20,4
	19,9	20,0	20,3	20,2	21,0	20,1	20,3	20,5	20,4	19,8	20,6
	19,7	19,8	20,0	20,1	19,7	20,3	20,2	20,1	20,4	20,5	20,7
	20,3	20,5	20,2	20,5	20,7	21,0	21,1	19,5	20,2	20,4	20,9
	19,5	19,8	20,0	20,1	20,4	20,5	20,3	20,6

 

8.19.

 

8.20.